
설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
통합검색


Search Close

설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
임의 물체를 전자 현미경으로 확대해 보면 무수히 많은 작은 입자들이 서로 결합되어 있는 것을 볼 수 있다. 이처럼 모든 물체는 그 물체를 구성하는 기본 입자들의 결합체이다.
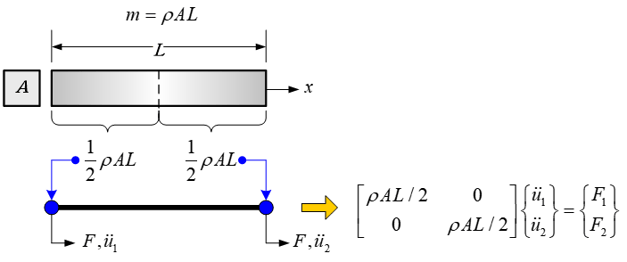
한편, 임의 물체의 질량은 외부로부터 힘을 받았을 때 물체의 위치나 속도의 변화에 저항하려는 정도를 나타낸다. 질량이 클수록 물체는 외부로부터 힘을 받았을 때 위치나 속도 변화에 대한 저항력이 비례적으로 증가한다. 그리고 한 물체의 질량은 그 물체를 구성하는 모든 입자들의 질량의 총 합과 같다. 따라서 한 물체의 질량은 그 물체 내부에 연속적으로 분포되어 있다. 집중질량은 물체 내부의 특정 영역에 분포되어 있는 입자들을 이 영역 내 임의 한 점에 모여있다고 가정하고, 그 지점에 집중시킨 가정한 가상적인 질량이다.
한편, 물체를 이루는 전체 입자들을 물체 내 임의 한 지점에 모여있다고 가정하면, 물체는 이 지점에 집중된 질량을 갖는 하나의 점으로 표현된다. 집중질량은 물체의 운동이나 힘 그리고 모멘트 등의 계산을 매우 편리하게 해 준다. 하지만, 물체 내부에 연속적으로 분포되어 있는 질량을 물체 내 임의 한 점 혹은 다수의 지점으로 집중시키기 때문에 물체의 운동이나 힘 그리고 모멘트 등의 계산에 있어서 정확도는 떨어진다.
집중질량을 적용할 때 고려해야 할 중요한 조건은 집중시킨 질량의 총 합은 집중시키지 않은 물체의 원래 질량과 같아야 한다는 점과, 집중시킨 질량의 정적 그리고 동적인 효과는 집중시키지 않은 경우와 큰 차이를 나타내지 않아야 한다는 점이다.
.
IGES는 컴퓨터를 이용한 형상 모델링 및 설계, 즉 CAD(computer-aided design)에 사용되는 Data 양식에 대한 표준을 정의하는 규정으로서 Initial Graphics Exchange Specification의 약자이다. 이러한 표준은 CAD Data 파일을 서로 주고 받을 때 아무런 문제없이 호환될 수 있도록 하기 위하여 제정되었다. 다시 말해 A라는 사람이 자신이 사용하고 있는 CAD 프로그램에서 생성한 Data 파일을 B라는 사람이 건네 받아 자신이 사용하고 있는 유형이 다른 CAD 프로그램에서 아무런 문제없이 작업을 수행할 수 있도록 하기 위함이다.
IGES 표준에는 circuit 다이어그램, 와이어 프레임(wireframe), 형상모델 표현 등과 같은 형상 모델링 작업뿐만 아니라 도면 작업 그리고 해석을 위한 모델생성 및 제작을 위한 Data에 형식에 이르기 까지 제반사항에 대한 기준을 정의하고 있다. IGES는 1980년 미국 표준청(US National Bureau of Standards)에 의해 DRCPDD라는 공식적인 명칭으로 출판되었으며, 미국 기계학회의 ASME Y14.26M으로 언급되었었다.
IGES 표준화 사업은 미국의 보잉사, GE, Xerox 등과 같은 업체와 미국 표준청 및 미국방성(DoD: US Department of Defense) 그리고 CAD 사용자 그룹에 의해 1979년에 최초로 시작되었다. 1980년에 초기 표준이 출판된 이후 표준에 대한 보완이 지속적으로 이루어 지고 있다.
.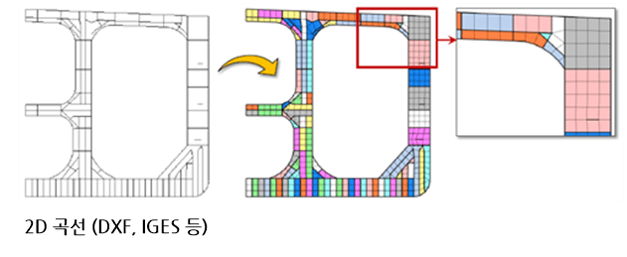
유한요소 해석을 위해 대상이 되는 물체의 기하학적 영역을 여러 개의 작은 세부 영역들로 쪼개는 작업을 요소망(mesh)을 생성한다고 말한다. 그리고 각각의 세부 영역들을 유한요소(finite element)라고 부르는데, 이와 같이 요소망을 생성하는 이유는 구하고자 하는 물체의 거동을 근사하기 위해 사용되는 기저함수(basis function)를 아무리 물체의 형상이 복잡하더라도 체계적이고 효과적으로 정의하기 위함이다. 그리고 유한요소법이라는 이름이 붙여지게 된 근원이 바로 여기에 있다.
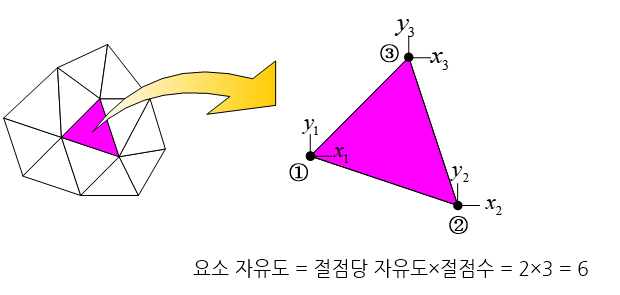
각각의 요소는 절점(node)이라 불리는 특정한 점들을 가지고 있는데, 이 절점들에서 물체의 거동값을 계산하여 요소망 전체에 걸친 거동의 전체 분포를 최종적으로 표현(근사)한다. 한편, 각 절점에서의 물체의 거동값은 물체 거동을 계산하기 위해 수치적으로 변환시킨 행렬 방정식의 미지수, 즉 자유도(degree of freedom)에 해당된다.
한 절점이 가지게 되는 미지수의 개수를 절점 자유도(nodal degree of freedom)라고 부르며, 풀고자 하는 물체 거동의 유형에 따라 달라진다. 요소 자유도란 한 요소내 각 절점에서의 자유도를 모두 합한 자유도를 의미한다. 예를 들어 절점 자유도가 3인 4개의 절점으로 구성되어 있는 사각형 요소의 요소 자유도는 12가 된다.
.
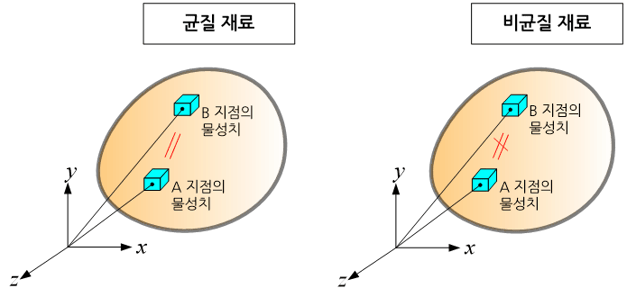
어떤 재료가 균질하다는 것은 재료 내 각 지점에서 재료의 물성치가 동일하다는 것을 의미한다. 엄밀한 의미에서 균질한 재료는 존재하지 않는다. 왜냐하면 재료를 전자현미경으로 들여다 보면 구성 입자들의 형상, 크기 그리고 결합되어 있는 조직이 일정하지 않기 때문이다. 하지만 재료를 균질하다고 가정하는 것은 이러한 미세한(micro) 구성 입자 수준을 의미하는 것이 아니라, 재료의 물성이 거시적(macro)인 측면에서 측정하였을 때 그 값들이 재료 내 각 지점에서 거의 동일하다는 것을 의미한다. 단일 재질로 구성되어 있는 대부분의 금속, 플라스틱, 유리 등은 균질한 재료로 가정한다. 균질하지 않은 대표적인 재료로는 두 가지 이상의 재질로 구성되어 있는 복합재를 들 수가 있다.
참고로 균질성과 함께 재료를 크게 구분하는 용어에는 등방성(isotropy)과 이방성(anisotropy)이 있다. 이 용어는 재료의 물성치가 위치에 따라 균일한가 아닌가를 판단하는 것이 아니라, 방향에 따라 재료 물성치(material property)가 불변인가 그렇지 않은가를 구분하기 위해 사용된다.
.
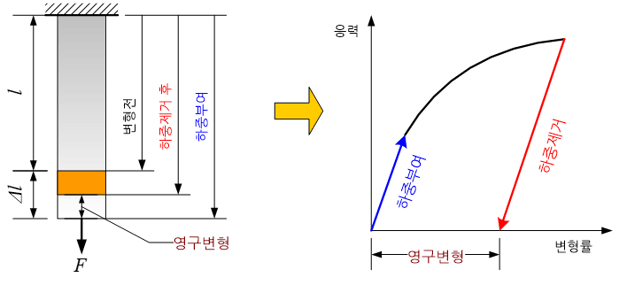
물체는 힘이나 열과 같이 외부로부터 자극을 받으면 그 형상이 변하는 변형(deformation)을 일으킨다. 물체는 외부로부터 자극을 받으면 변형에 저항하려는 성질과 변형을 그대로 유지하려는 두 가지 상반된 성질을 나타낸다. 전자를 탄성 (elasticity)이라고 부르고 후자를 소성(plasticity)이라고 부른다.
탄성은 외부로부터 받은 자극이 제거되면 물체를 원래 형상으로 복원시키려는 성질인 반면, 소성은 외부의 자극이 제거되어도 변형을 그대로 유지하려는 성질이다. 모든 물질은 이 두 가지 성질을 지니고 있으며, 외부 자극의 크기에 따라 두 성질 중 어느 것이 우세한지가 좌우된다.
일반적으로 외부 자극이 커질수록 소성이 증가한다. 이 특성을 이용한 대표적인 것이 금속 판을 구부리거나 찍어서 원하는 형상의 제품으로 가공하는 것이다. 자동차를 위시한 대부분의 조립체를 구성하는 부품들은 소성을 이용하여 원하는 형상으로 변형시켜 가공한 것들이다.
참고로 외부 자극이 커질수록 소성이 증가하지만, 미소한 량의 탄성은 여전히 남아있다. 그래서 물체에 변형을 가하여 원하는 형상으로 만들었다고 하더라도 외부 자극을 제거하면 어느 정도 원래 모양으로 복원하려는 스프링 백(spring back) 거동을 나타낸다. 따라서 소성변형을 이용하여 부품을 제작하고자 할 경우, 이 스프링 백 량을 미리 예측하여 구부리거나 찌그러뜨리는 량을 결정해야 한다.
.
설계업무를 수행하다 보면 형상은 동일하지만 가해지는 하중조건(load condition)만 달라지는 경우가 종종 있다. 다시 말해, 하나의 대상 물체에 있어 물체에 작용하는 하중이 달라짐에 따라 물체의 거동이 어떻게 변화하는지가 관심사가 되는 경우가 종종 발생한다.
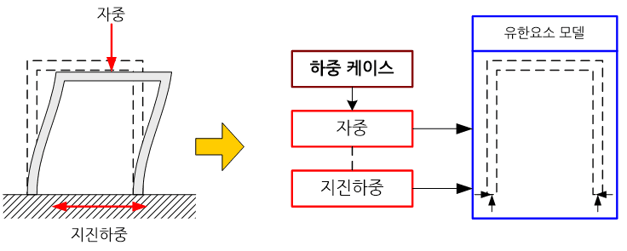
고층건물이 자중에 의해 얼마나 변형(deformation)하는지, 지진에 의해서는 얼마나 변형하는지, 그리고 자중과 지진파를 동시에 고려하였을 경우에는 또 변형이 어떻게 되는지를 각각 계산하여 그 결과를 비교하고자 하는 경우를 예를 들어 보자. 이러한 경우, 물체의 기하학적 형상, 재료 물성치(material property), 요소망(mesh) 그리고 변위 구속조건(displacement boundary condition)은 동일하지만, 하중조건만 달라지게 된다. 이러한 해석문제를 효과적으로 수행하기 위한 방법으로 다중 해석(multi-analysis)이라는 수치기법이 있으며, 거의 대부분의 상용 유한요소 해석 프로그램에서 이 기능을 지원하고 있다.
이 기법에서는 하중조건을 설정하는 것 이외에는 하나의 해석문제를 취급하는 일반 유한요소 해석과 그 절차와 방법이 동일하다. 하지만 다루고자 하는 각각의 하중조건을 각기 하나의 하중 케이스(load case)로 설정하여 여러 하중 케이스를 준비해야 한다. 그리고 각각의 하중 케이스를 불러들여 유한요소 해석을 각각 수행하기만 하면 원하는 여러 하중 조건에 대한 물체의 거동을 빠른 시간 내에 효과적으로 구할 수 있다. 이와 같이 각기 독립적으로 설정된 여러 하중 케이스들을 특별히 다중 하중 케이스라고 부른다.
.
우리 주위에서 흔히 볼 수 있는 물체의 거동은 물체 내 위치에 따라 그 거동이 변할 뿐만 아니라 시간과 더불어 변하는 경우가 많다. 시간과 무관하게 물체 내 공간상의 위치에 따른 거동을 분석하는 경우를 경계치 문제, 그리고 물체 내 일정한 지점에서 시간에 따라 변하는 물체의 거동을 분석하는 것을 초기치 문제(initial value problem)로 구분하고 있다. 하지만 자연계 대부분의 현상은 그 거동이 공간상의 위치뿐만 아니라 동시에 시간에 따라서도 변하기 때문에 경계치-초기치 문제(boundary and initial value problem)로 볼 수 있다.
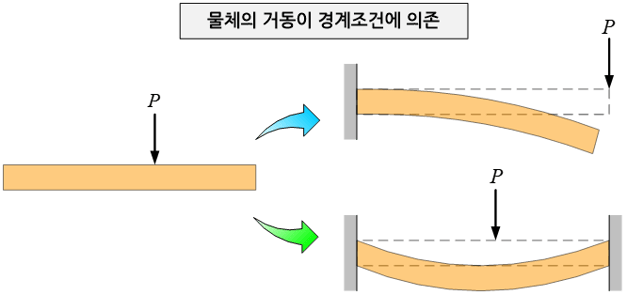
예를 들어, 고층건물이 자체 무게에 의해 얼마나 큰 응력(stress)이 내부에 발생하는가 하는 문제는 경계치 문제에 해당되고, 고층건물 내 특정한 부위가 지진파에 따라 시간적으로 어떻게 거동할 것인가는 초기치 문제에 해당된다. 그리고 지진파에 따라 고층건물 전체의 변형이나 응력이 시간과 더불어 어떠한 변동을 나타내는가 하는 문제는 경계치-초기치 문제에 해당된다. 시간과 무관하게 물체 내 위치에 따른 거동을 분석하는 것을 경계치 문제라고 부르는 이유는, 물체 내 거동이 물체의 경계, 즉 외부와 직접 접하고 있는 물체의 표면에 가해지는 각종 구속조건과 경계조건(총칭하여 경계조건(boundary condition)이라 부름)에 의해 절대적으로 좌우되기 때문이다. 예를 들어 한 쪽 끝 단이 벽에 고정되어 있는 가느다란 나무막대를 생각해 보자. 다른 쪽 끝 단에 수직하중을 가하는 경우와 다른 한 쪽 끝 단도 동시에 지지하면서 막대의 가운데에 수직하중을 가하는 두 경우에 있어서 막대가 변형(deformation)되는 모양은 판이하게 다르다.
이처럼 경계치 문제에 해당되는 물체의 거동은 경계조건에 주도적인 영향을 받는다. 따라서, 이러한 문제를 유한요소 해석(finite element analysis)으로 풀고자 할 경우, 해석결과의 신뢰성은 경계조건을 얼마나 정확하게 반영하느냐에 달려있다고 하여도 과언은 아니다.
.
코일 스프링을 길이 방향으로 잡아당기거나 누르면 길이가 늘어나거나 줄어든다. 늘어나거나 줄어드는 길이는 스프링의 강한 정도, 즉 강성(stiffness) 혹은 스프링 상수(spring constant)에 반비례하고 스프링에 가한 하중(load)에 비례한다. 임의 3차원 물체는 이러한 스프링이 무수히 많이 빽빽하게 차여있는 물체라고 생각할 수 있다. 따라서 임의 물체가 외부로부터 힘을 받아 늘어나거나 줄어드는 길이, 즉 변형은 외력의 크기에 비례하고 물체의 강성에 반비례한다.
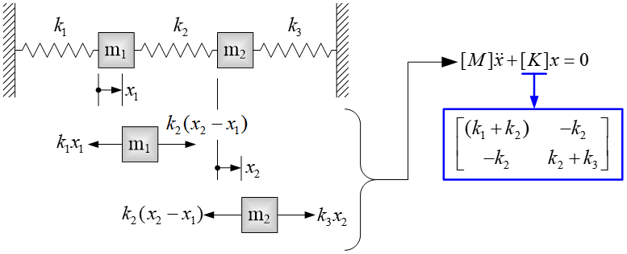
물체의 변형이 외력 및 강성에 비례적인 관계를 보이는 경우를 선형(linear)이라고 말한다. 선형적인 정적 거동(static behavior)을 나타내는 물체에 유한요소법(finite element method)을 적용하면 [K]{u}={F}라는 행렬방정식을 푸는 수치해석 문제로 변환된다. 여기서 행렬 [K]를 강성행렬, 행렬 {F}를 하중벡터(load vector), 그리고 행렬 {u}는 구하고자 하는 미지수, 즉 물체의 근사적인 변형 값이다.
행렬의 이름을 이처럼 부르게 된 것은 위에서 설명한 코일 스프링의 역학적 거동에서 유래되었다. 코일 스프링과 마찬가지로 강성행렬은 물체의 강한 정도를 나타내며, 물체의 재질, 두께 및 구조에 따라 결정된다. 강성행렬은 요소망(mesh) 내 각 유한요소 별로 계산하여 모두 합하는 방식으로 계산되며, 각 유한요소 별 강성행렬을 특별히 요소 강성행렬(element stiffness matrix)이라고 부른다.
.
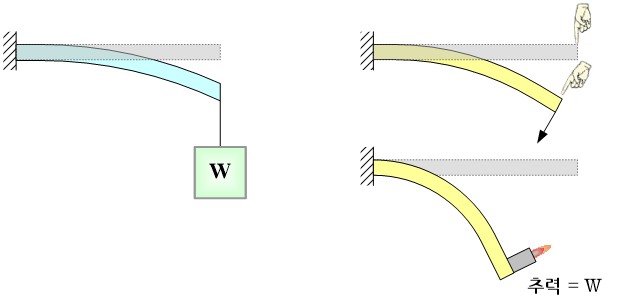
힘의 특수한 경우로서, 물체의 변형에 따라 그 방향이 변하는 힘을 의미한다.
왼 쪽 끝단이 벽에 고정되어 있는 가느다란 나무판자를 예를 들어 비교해 보자. 오른 쪽 끝단에 물체를 올려 놓으면 나무판이 변형되어 오른 쪽 끝단이 아래로 기울어 지더라도 물체의 자중은 변함없이 정확히 아랫 방향을 향한다. 따라서 이 경우에 있어 물체의 자중은 종동력이 아니다. 하지만 우측 끝 단을 손가락 끝으로 수직으로 힘을 가한다면 판자가 기울어지더라도 손가락은 판자와 수직이 되어야 하므로 손가락이 누르는 힘의 방향은 변하게 된다. 따라서 이 경우가 종동력에 해당된다.
종동력은 비선형성(nonlinearity)을 나타낸다. 왜냐하면, 힘의 방향은 물체의 변형에 의해 결정되기 때문이고, 이 물체의 변형은 다시 힘에 의해 결정되기 때문이다. 다시 말해, 물체의 변형을 계산하기 위해 필요한 하중의 방향이 아직 구하지 않은 물체 변형의 함수로 표현된다. 하지만 하중 방향의 변화가 그다지 심하지 않은 경우에는 비선형 해석(nonlinear analysis)을 피하기 위하여, 방향 변화를 무시하고 선형해석(linear analysis)으로 단순화 시키는 것이 일반적이다.
.
해석 정확도를 높이고, 반복 작업을 줄여보세요.
내게 맞는 솔루션 찾기