임의 단면을 가진 가느다란 물체에 힘을 가하여 잡아당기면 물체는 힘을 받는 방향으로 늘어난다. 그리고 프와송 효과(Poisson’s effect)에 의하여 물체의 단면적은 감소한다. 외부 하중에 저항하는 물체 내부의 저항력인 응력(stress)은 하중을 물체의 단면적으로 나눈 값으로 정의된다. 하지만 물체의 단면적은 하중이 증가할수록 점차적으로 감소한다.
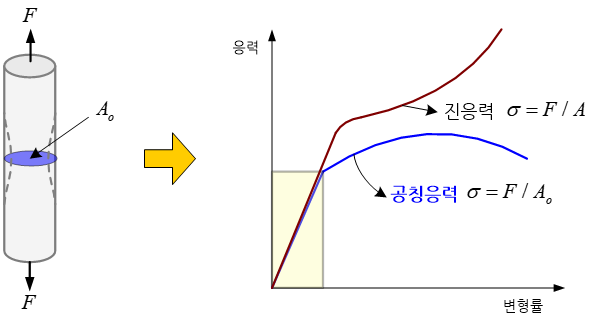
가느다란 금속 판을 한 방향으로 하중을 가하여 응력을 측정하는 경우를 예로 들어 보자. 물체의 단면적을 물체가 변형되기 전 초기 단면적으로 외부 하중을 나누어 응력값을 계산하는 방법과 변형에 의해 감소된 실제 단면적으로 응력값을 계산하는 두 가지 방안이 있을 수 있다. 전자의 방법으로 구한 응력을 공칭응력이라고 부르고, 후자의 방식으로 구한 응력을 진응력(true stress) 이라고 부른다. 당연히 진응력이 정확한 의미의 응력이고, 변형이 커질수록 두 값의 차이도 커진다. 특히, 물체가 끊어지기 직전에는 단면적이 매우 작아지기 때문에 진응력은 매우 큰 값이 되는 반면 공칭응력은 단면적의 감소를 반영하지 않기 때문에 하중 증가만큼 증가할 뿐이다.
하지만 실제 상황에서 이처럼 극단적인 경우는 그다지 많지 않고, 대부분의 경우 변형량은 크지 않다. 따라서 공칭응력을 많이 사용하고 있는 실정이다. 유한요소 해석(finite element analysis)에서 선형해석으로 구한 응력값은 공칭응력에 해당되고, 비선형 해석(nonlinear analysis)으로 구한 응력은 진응력에 해당된다고 볼 수 있다. 왜냐하면, 전자는 변형되기 전 초기 물체의 형상을 기준으로 단 한번의 계산으로 응력을 구하기 때문에 물체의 변형이 반영될 수 없다. 하지만 비선형 해석에서는 하중을 조금씩 증가시키면서 반복적으로 변형률(strain)과 응력을 계산하기 때문에 물체의 변형이 반복계산 과정에서 반영될 수 있기 때문이다.
.