CAE 입문자도 쉽게 이해할 수 있는 '알기 쉬운 기술 용어집'
CAE 관련 용어를 확인해 보세요.
반도체 / 디스플레이 공정 및 장비 관련 용어를 확인해 보세요.
통신 분야의 다양한 용어를 확인해 보세요.
어떠한 자연 현상을 수학적으로 표현하고, 이 수학적 표현을 수식으로 전환하여 계산기나 컴퓨터를 이용하여 계산한 결과는 숫자 형식의 데이터이다. 예를 들어 차량이 지나다니는 교량의 변위(displacement)를 계산하면 교량 각 지점에서의 변위값을 구할 수 있다. 요즘과 같이 컴퓨터 그래픽스(computer graphics) 기술이 발달하기 이전에는 숫자 형식의 방대한 변위값을 용지에 기록하여 교량의 위치와 그 지점에 해당하는 변위값을 일일이 확인하였다. 그리고 이 숫자 형식의 변위값을 토대로 변형(deformation), 변형률(strain) 및 응력(stress) 등을 계산기를 이용하여 일일이 수작업으로 계산하였다.
이렇게 계산 결과를 분석하는 것도 좁은 의미에서 후처리 작업으로 볼 수 있다. 하지만 컴퓨터 그래픽스 기술이 보편화 되어 있는 지금에 있어서 후처리 작업의 정의는 보다 광범위하다. 수식을 계산하여 구한 숫자 형식의 변위값을 컴퓨터 화면상에 가시적으로 나타내면 교량 전체의 변형된 형상을 한 눈에 생생하게 볼 수 있다. 그리고 변위와 변형률 그리고 변형률과 응력과의 관계식을 이용하여 교량 전체에 대한 변형률, 응력 등의 분포를 가시화 시킬 수 있다.
그 뿐만 아니라 마우스를 이용하여 교량의 특정 위치를 선택하면 해당 지점에서의 변위, 변형률, 응력 등의 상세 수치값을 쉽게 확인할 수 있다. 또한 원하는 유형의 결과값을 그래프 형식으로 볼 수 있을 뿐만 아니라 결과값을 프린터를 통하여 출력하거나 저장 매체에 보관할 수도 있다. 또한 결과값을 토대로 교량의 안전성과 같은 설계 사양들을 분석할 수도 있다.
이렇게 수식을 계산한 후 그 계산 결과를 다양한 형태로 모니터 화면상에 가시화 혹은 조회하거나 목표로 하는 성능들을 분석하고, 프린터 혹은 저장매체를 통해 출력하는 제반 작업을 광의적인 의미에서 후처리라고 한다. 그리고 소프트웨어 내부에서 이 후처리 기능을 담당하는 부분을 후처리기라고 부른다.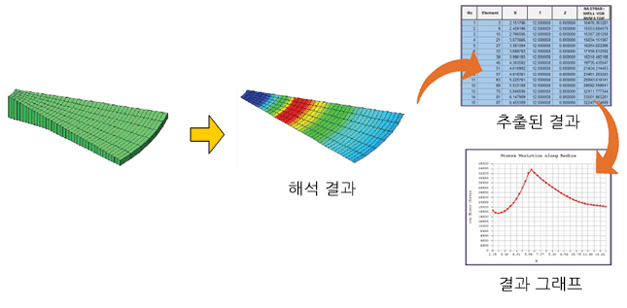
물체에 하중을 가할 경우 물체가 늘어나는 크기인 변형률(strain)과 물체 내부에 발생하는 저항성분인 응력(stress)과의 관계를 그래프로 나타낸 것을 응력-변형률 선도(stress-strain diagram)이라고 부른다. 이 그래프는 관심이 되는 물체의 시편(specimen)을 만들어 인장시험기라고 부르는 실험장치를 이용하여 구할 수 있다.
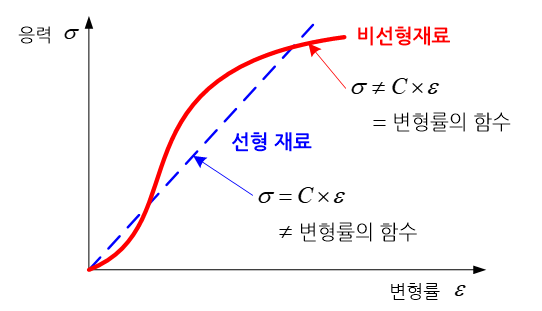
만일 변형률과 응력이 선형적인 관계, 다시 말해 두 값이 일정한 기울기를 가지고 변한다면 그 물체는 선형적인 거동을 나타낸다고 말한다. 대부분의 물체에 있어서, 변형률이 미소한 경우에는 이러한 선형적 가정을 적용하여도 무방하다. 하지만 변형률이 커지게 되면 응력과 변형률은 더 이상 선형적인 관계를 나타내지 않는다. 참고로 고무와 같은 초탄성 재료(hyperelastic material)는 아주 작은 변형률에서도 현저한 비선형적 관계를 나타낸다.
이와 같이 변형률과 응력이 비선형적인 관계를 나타내는 물체를 재료 비선형이라고 부르고, 비선형 해석(nonlinear analysis)에 있어 상당부분을 차지하고 있다. 금속과 같은 전형적인 재료는 항복응력(yield stress)에 도달하기 이전까지를 선형 재료 그리고 이 지점 이후를 비선형 재료로 가정한다.
재료 비선형 물체의 응력-변형률 관계를 표현하기 위한 재료모델(material model)에는 다양한 종류가 소개되어 있다. 고무와 같은 재료를 위한 문리-리브린 모델(Moonley-Rivlin model), 소성변형(plastic deformation)을 나타내는 재료를 위한 멱법칙(power law) 모델 등이 대표적인 예이다.
.
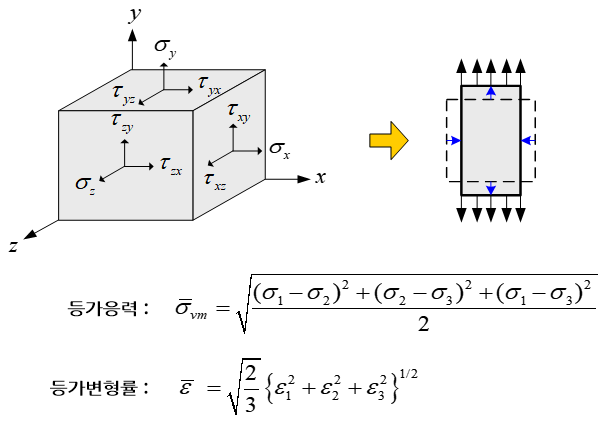
외부로부터 하중을 받고 있는 임의 물체에 있어 그 내부에 발생하는 저항력인 응력(stress)은 방향별 성분을 지니고 있다. 따라서 물체내 임의 지점에서 응력의 절대적인 크기는 임의 응력 성분 하나만으로는 결정할 수 없다. 폰 미제스 응력(von Mises stress)으로 불리는 등가응력(equivalent stress)은 임의 지점에서의 응력의 절대적인 크기를 나타내기 위해 가장 많이 사용되고 있다.
응력과 마찬가지로 물체 변형의 크기를 나타내는 변형률(strain)도 방향별 성분을 지니고 있기 때문에 어느 한 성분만으로 변형률의 절대적인 크기를 나타낼 수 없다. 따라서 물체 내 임의 지점에서 변형률의 절대적인 크기를 나타내기 위한 척도가 필요하다. 등가 변형률은 이러한 변형률의 절대적인 크기를 나타내는 척도로 사용되고 있고 있으며, 물리적으로 등가응력과 짝을 이루는 물리량으로 생각할 수 있다.
보다 정확한 표현으로 등가 변형률은 편차응력(deviatoric stress)과 역학적으로 관계를 맺는다. 등가 변형률은 변형률 성분 각각의 제곱을 모두 합한 값에 2/3를 곱하여 제곱근을 취하여 계산되며, 금속성형(metal forming)과 같은 소성변형(plastic deformation) 거동을 표현하는 소성모델(plastic model)의 변수로 사용되고 있다.
.
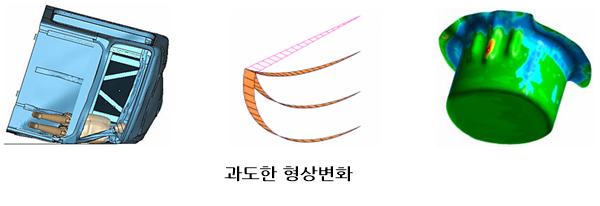
외부로부터 하중이나 모멘트를 받는 물체에 있어 물체의 변위나 회전(rotation)이 과도한 경우, 물체는 현저한 비선형성(nonlinearity)을 나타낸다. 보통 대변형 문제라고 부르는 것은 변위와 회전 그리고 변형률 모두가 큰 값인 경우를 의미한다. 하지만 대 변위 혹은 대 회전이라고 해서 반드시 변형률(strain)이 크다고는 단정지을 수 없다. 왜냐하면, 변위나 회전량은 클지라도 변형률 자체는 작을 수 있기 때문이다.
예를 들어, 한 쪽 끝 단이 벽에 고정되어 있는 얇은 금속판의 다른 끝 단에 집중하중을 가하는 경우를 생각해 보자. 하중이 증가하면 금속 판재는 마치 동그랗게 말리는 것과 같은 대 변위와 대 회전을 나타낸다. 하지만 금속 판재 내 각 점의 상대거리의 변화는 그다지 크지 않아 변형률은 크지 않다. 따라서 대 변위 혹은 대 회전 문제는 대 변형률과 미소 변형률 문제로 다시 세분화 할 수 있다. 어떠한 경우라 할지라도 대 변위 혹은 대 회전 문제는 기하학적 형상의 과도한 변화로 인하여 현저한 비선형성(nonlinearity)을 야기한다. 또한 물체에 가해지는 하중이나 모멘트의 크기는 일정하게 유지될지라도 그 방향이 형상에 따라 변할 수 있는, 다시 말해 종동력(follower force) 형태가 될 수도 있다.
이와 같이 물체의 기하학적 형상이 크게 변함에 따라 수반되는 비선형성을 기하 비선형이라고 정의하고 있다. 기하 비선형 문제의 유한요소 해석을 위해서는 토탈 라그랑지언(total Lagrangian) 혹은 업데이티드 라그랑지언(updated Lagrangian) 방식에 따라 문제를 정의할 수 있으며, 전자의 경우에는 코오시 응력(Cauchy stress) 대신 물체의 변형 전 초기형상으로 변환시킨 가상적인 응력인 피올라-킥컵응력(piola-Kirchhoff stress)이 사용된다.
.
고무와 같은 재료는 조그마한 하중에도 매우 큰 변형을 나타낸다. 따라서 고무와 같은 재료의 구조적 상실을 판단하기 위해서는 응력(stress)이 아닌 변형률(strain)이 주로 사용된다. 특히, 반복하중을 받는 고무제품의 피로에 의한 구조적 파괴를 예측하기 위해서는 응력을 기준으로 한 S-N 선도(S-N diagram)가 아닌 변형률을 기준으로 한 실험 데이터인 E-N 선도가 사용된다.
한편, 변형률도 응력과 같이 공간상에서 설정한 좌표축에 따라 성분을 가지기 때문에 물체내 한 지점에서의 변형률의 절대적인 크기를 계산하기 위한 잣대가 필요하다. 등가 변형률(equivalent strain)은 이러한 목적으로 정의된 물리량으로써 등가응력(effective stress, 혹은 폰 미제스 응력(von-Mises stress)) 과 짝을 이루는 량이다.
E-N 선도란 고무와 같이 극심한 대변형을 나타내는 재료의 피로수명(fatigue life)을 나타내는 선도로써, 해당 재료의 시편을 이용하여 실험적으로 구한 등가 변형률 대 피로수명 회수를 평가하기 위한 선도이다. 한편, S-N 선도를 이용하든지 아니면 E-N 선도를 이용하든지 간에 피로해석(fatigue analysis)의 방법과 절차는 동일하다.
.
정확한 것과 정확하지 않은 것과의 차이를 통칭하여 오차(error)라고 부른다. 오차를 말하기 위해서는 정확한 것이 명확히 정의되어야 하고, 또한 정확하지 않은 것과의 차이를 정의하는 방법이 결정되어야 한다.
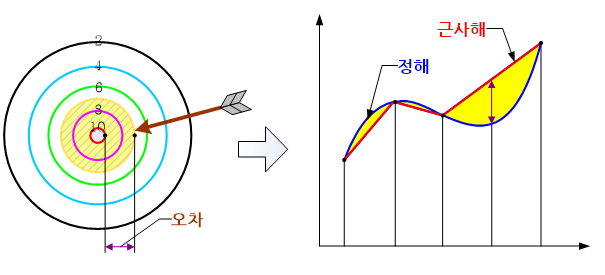
정확한 것의 정의와 정확하지 않은 것과의 차이를 정의하는 방법은 대상과 목적에 따라 각기 다르다. 예를 들어, 양궁 경기에 있어서 정확한 것은 과녁의 중앙 즉, 10점에 해당되는 가운데 영역을 맞히는 것이다. 그리고 정확하지 않은 것은 이 영역을 벗어난 과녁의 나머지 영역을 맞히는 것이다. 이 경우, 오차는 10점과 정확하지 않은 영역에 지정되어 있는 점수와의 차이로 계산된다.
한편, 유한요소 해석(finite element analysis)에 있어 정확한 것은 해당 문제에 대한 이론적인 정해(exact solution)를 의미하며, 정확하지 않은 것은 이론적으로 구한 것이 아닌 수치해석적으로 구한 근사해(approximate solution)를 의미한다. 그리고 오차는 정해와 근사해와의 차이로 일반적으로 좌표 혹은 시간의 함수로 표현된다. 하지만 이것은 개념적인 의미이고 보다 실제적인 의미에서의 오차는 그 차이를 어떻게 정의하는냐에 따라 다양하다.
예를 들어 물체의 변형(deformation), 변형률(strain) 및 응력(stress)을 계산하는 경우를 생각해 보자. 물체 내 최대 변형값의 차이를 오차로 정의할 수도 있고, 최대 응력값의 차이를 오차로 정의할 수도 있다. 전자의 경우는 물체의 최대 변형이 관심이 되는 경우이고 후자는 물체의 강도가 관심이 되는 경우이다. 이처럼 유한요소 해석에서 오차의 정의는 유한요소 해석을 수행하는 목적에 따라 결정된다. 다시 말해 동일한 해석문제에 있어서도 해석의 목적이 달라지면 오차 정의도 그에 따라 달라질 수 있다.
.
외부로부터 물체에 힘을 가하여 변형시키면 외력이 한 총 일은 물체의 변형 경로와는 무관하게 최종 변형 상태에만 의존하는 경우가 있다. 다시 말해 물체에 힘을 가하여 초기 상태로부터 일련의 변형 상태를 거쳐 다시 초기상태로 되돌아 오도록 한다면 외부 힘이 한 일은 없다.
이렇게 외력에 의한 일이 경로에 무관하게 되면 포텐셜 함수(potential function)가 존재하게 되고 이 포텐셜 함수의 변화율이 다름아닌 하중에 해당된다. 그리고 이러한 포텐셜 함수가 존재하는 물체의 변형을 가역적(reversible)이라고 부르고 포텐셜 함수의 변화율로 표현되는 힘을 보존력(conservative force)으로 정의한다.
탄성재료(elastic material)의 경우 포텐셜 함수는 물체의 변형에 따라 내부에 축적되는 단위 체적당 변형률 에너지로 불리는 변형률 에너지 밀도(strain energy density)이다. 그리고 탄성재료 중에서 응력(stress)을 변형률 에너지 밀도로부터 유도할 수 있는 재료를 특별히 초탄성 재료로 분류한다.
초탄성 재료의 가장 대표적인 예는 고무로서, 외부로부터 힘을 받으면 내부에 발생하는 저항력인 응력은 고무의 변형에 따라 내부에 축적되는 변형률 에너지 밀도를 이용하여 계산할 수 있다. 다시 말해 변형률 에너지 밀도의 변형률(strain)에 대한 상대적인 변화율이 응력에 해당된다.
.
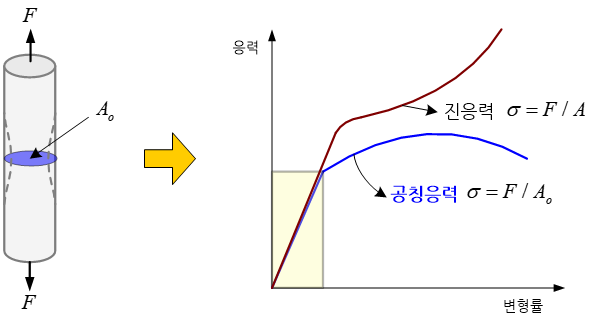
임의 단면을 가진 가느다란 물체에 힘을 가하여 잡아당기면 물체는 힘을 받는 방향으로 늘어난다. 그리고 프와송 효과(Poisson’s effect)에 의하여 물체의 단면적은 감소한다. 외부 하중에 저항하는 물체 내부의 저항력인 응력(stress)은 하중을 물체의 단면적으로 나눈 값으로 정의된다. 하지만 물체의 단면적은 하중이 증가할수록 점차적으로 감소한다.
가느다란 금속 판을 한 방향으로 하중을 가하여 응력을 측정하는 경우를 예로 들어 보자. 물체의 단면적을 물체가 변형되기 전 초기 단면적으로 외부 하중을 나누어 응력값을 계산하는 방법과 변형에 의해 감소된 실제 단면적으로 응력값을 계산하는 두 가지 방안이 있을 수 있다. 전자의 방법으로 구한 응력을 공칭응력이라고 부르고, 후자의 방식으로 구한 응력을 진응력(true stress) 이라고 부른다. 당연히 진응력이 정확한 의미의 응력이고, 변형이 커질수록 두 값의 차이도 커진다. 특히, 물체가 끊어지기 직전에는 단면적이 매우 작아지기 때문에 진응력은 매우 큰 값이 되는 반면 공칭응력은 단면적의 감소를 반영하지 않기 때문에 하중 증가만큼 증가할 뿐이다.
하지만 실제 상황에서 이처럼 극단적인 경우는 그다지 많지 않고, 대부분의 경우 변형량은 크지 않다. 따라서 공칭응력을 많이 사용하고 있는 실정이다. 유한요소 해석(finite element analysis)에서 선형해석으로 구한 응력값은 공칭응력에 해당되고, 비선형 해석(nonlinear analysis)으로 구한 응력은 진응력에 해당된다고 볼 수 있다. 왜냐하면, 전자는 변형되기 전 초기 물체의 형상을 기준으로 단 한번의 계산으로 응력을 구하기 때문에 물체의 변형이 반영될 수 없다. 하지만 비선형 해석에서는 하중을 조금씩 증가시키면서 반복적으로 변형률(strain)과 응력을 계산하기 때문에 물체의 변형이 반복계산 과정에서 반영될 수 있기 때문이다.
.
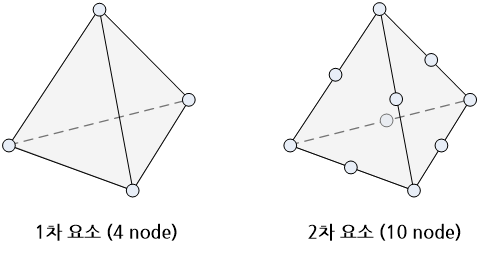
유한요소 해석을 위해 물체가 차지하고 있는 기하학적 영역을 세분화시키는 요소망(mesh) 생성에 필요한 유한요소(finite element)의 한 종류이다. 유한요소는 차원, 형상 및 차수에 따라 분류할 수 있는데, 사면체 요소는 3차원 요소들 중에서 가장 기본이 되는 유형으로서, 쐐기 형상으로 4개의 면으로 구성되어 있다. 사면체 요소는 차수에 따라 1차 요소는 각 꼭지점에 하나씩 절점을 지닌 4절점 요소 그리고 2차 요소는 각 꼭지점과 변에 하나씩 절점을 가진 10절점 요소로 다시 구분된다.
사면체 요소는 임의 형상을 지닌 3차원 물체의 요소망 생성에 반드시 필요한 기본적인 요소이다. 왜냐하면, 오면체(pentahedron)와 육면체(hexahedron) 요소만으로는 요소망을 생성할 수 없는 경우가 종종 발생하기 때문이다. 예를 들어 3차원 구(sphere) 형상의 물체를 오면체와 육면체 요소로 세분화 하는 경우를 생각해 보면 쉽게 이해할 수 있을 것이다.
사면체 요소 중에서 1차 요소에 해당되는 4절점 요소는 일정 변형률 요소(constant strain element)의 한 유형으로서, 물체 변형에 따른 변형률(strain)이 이 요소 내에서 일정한 값을 가지게 된다. 그 결과 잠김현상(locking phenomenon)과 같은 해석 정확도(analysis accuracy)의 저하를 유발시킨다. 따라서, 4절점 사면체 요소는 불가피한 상황이 아닌 경우에는 사용하지 않는 것이 좋다.
.
