
설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
통합검색


Search Close

설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
유한요소해석(finite element analysis)을 통해 임의 물체의 거동을 분석하는 경우, 구하게 되는 근사해(approximate)의 정확도가 원하는 수준에 미치지 못하는 경우가 많다. 근사해의 정확도는 오차평가(error estimate)라 불리는 특별한 기법이나 이론적인 정답 혹은 실험결과와의 비교 등을 통하여 수행된다.
그리고 근사해의 정확도는 요소망(mesh)의 조밀도 혹은 유한요소(finite element)에 적용되는 기저함수(interpolation function)의 차수 그리고 입력 값으로 입력되는 재료 물성치(material properties), 경계조건(boundary condition), 그리고 수치기법과 관련된 각종 수치 파라메터(parameter)에 의하여 좌우된다.
적응적 유한요소 해석이란 원하는 정확도를 만족하는 근사해를 구하기 위하여 이러한 값들을 조절하면서 오차(error)를 줄여가는 일종의 반복해석 과정을 말한다. 흔히 요소망의 밀도와 기저함수의 차수를 조정하게 되는데, 보다 합리적으로 조정하기 위하여 선 오차평가(a priori error estimate)와 후 오차평가(a posteriori error estimate)를 동시에 활용한다.
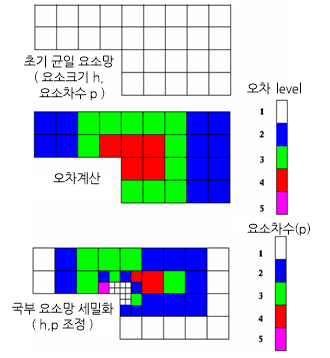
적응적 유한요소해석의 절차는 다음과 같이 구성된다. 우선 해석자가 초기에 설정한 요소망과 기저함수의 차수로 유한요소 해석을 수행하고, 해석결과의 정확성을 후 오차평가를 통하여 정량적으로 계산한다. 이렇게 계산된 오차값을 선 오차평가에 대입하여 원하는 정확도를 만족시킬 수 있는 유한요소의 크기(h)와 기저함수의 차수(p)를 계산한다.
계산된 유한요소의 크기와 기저함수의 차수를 적용하여 요소망을 세밀화(mesh refinement)한 다음 유한요소 해석을 재차 수행한다. 그리고 해석결과에 대한 정확도를 후 오차평가를 이용하여 재차 계산한다. 만일 여전히 원하는 정확도에 미치지 못하면 이러한 과정을 반복한다.
.
외부로부터 시간에 따라 변하는 동하중을 받는 물체나 구조물의 응답특성은 동하중의 크기(amplitude)뿐만 아니라 주파수(frequency)에도 지대한 영향을 받는다. 외란은 사인파(sine wave)나 코사인파(cosine wave)와 같이 단일 주파수를 가지는 경우도 있지만, 거의 대부분 주파수가 서로 다른 많은 파형들의 조합으로 이루어져 있다.
이러한 외란을 퓨리에 변환(Fourier transform)을 이용하여 주파수 영역으로 바꾸어, 주파수 영역에서 물체의 응답, 즉 주파수 응답해석(frequency response analysis)을 수행한다고 가정하자. 그러면 거의 연속적으로 분포되어 있는 모든 주파수 값에 대한 응답을 각각 구해야 한다. 하지만 이러한 작업은 계산시간 측면에서 비현실적이다.
따라서 일반적으로 중심 주파수(center frequency)라 불리는 주 관심 주파수를 중심으로 일정한 주파수 범위를 설정하고 이 범위 내에 포함되어 있는 주파수에 한정하여 응답을 구한다. 이렇게 설정한 주파수 영역을 관심 주파수 대역(frequency band)이라고 부르고, 주파수 응답의 목적에 따라 대역의 폭이 좌우된다. 그리고 이 주파수 대역에 포함되어 있는 주파수들에 대한 응답을 구하게 되는데, 이러한 작업은 마치 중심 주파수 값을 대역 내에서 좌우로 이동시켰을 때 물체의 응답이 어떻게 변화하는가를 분석하는 것과 같다.
이러한 맥락에서 주파수 스윕 해석이라고 부르고, 구체적인 계산방법에는 HFSS라 불리는 fast sweep과 discrete sweep이 있다. 전자는 계산시간을 최소화 하기 위해 중심 주파수와 대역의 좌우 끝점 주파수 값에 대한 응답을 구하여 대역 내 전체 주파수 응답을 개략적으로 구하는 방법이다. 반면, 후자는 대역 내에서 원하는 개수의 주파수 값을 선정하여 각 주파수에 대한 응답을 구하여 대역 전체에 대한 주파수 응답을 보간(interpolation)과 같은 곡선 맞춤(curve fitting)을 이용하여 근사화 시킨다. 일반적으로 fast sweep을 사용하면 discrete sweep에 비해 계산시간을 수십 배 이상 단축시킬 수 있다.
.
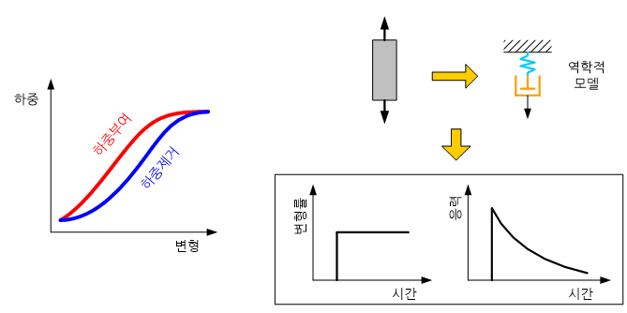
점성(viscosity)을 지니고 있는 탄성 물체를 의미하는 것으로, 콘크리트와 고무가 대표적인 재료이다. 이러한 물체는 하중을 받는 동안 변형률(strain)에 비례하여 응력(stress)이 증가하다가, 하중을 제거하는 시점부터 변형률은 일정하게 유지되지만 응력이 서서히 감소하는 특성을 나타낸다.
이러한 특성을 특별히 응력이완(stress relaxation)이라고 부르고 지수함수(exponential function) 형태의 감소 그래프를 나타낸다. 스프링 백(spring back) 현상이 하중을 제거하면 응력이 제거됨과 동시에 변형률이 어느 정도 감소하는 것과는 뚜렷이 구별된다. 점탄성 재료에 대한 역학적 모델은 스프링에 감쇠기(dashpot)를 직렬로 연결한 것으로 표현된다.
항복응력(yield stress)을 초과하는 하중상태에서의 점성효과를 점탄소성(visco-elastoplasticity)이라고 부르고, 역학적 분석이 매우 난해한 것으로 알려져 있다. 그 결과, 점탄성 해석은 대부분의 범용 유한요소해석 프로그램(general-purpose FEM program)이 지원하고 있지만, 점탄소성 해석은 일부 전용 유한요소해석 프로그램(special-purpose FEM program)에서만 제공되고 있는 실정이다.
점탄성 재료의 시간에 따른 응력이완 거동은 시간에 대한 프로니 급수 함수(Prony series function)로 표현되며, 이 함수에 포함되어 있는 프로니 상수(Prony constants)는 재료 시편을 이용한 실험 데이터를 최소자승법(least square method) 등으로 곡선 맞춤(curve fitting)을 통하여 결정된다. 따라서, 점탄성 해석은 하중이 가해지는 동안 탄성해석을 수행하여 하중이 가해지는 마지막 시점에서의 응력값을 구한 다음 이 응력값에 프로니 함수를 적용하는 방식으로 수행된다.
.
유한요소 해석(finite element analysis)에 있어 물체의 형상은 물체의 거동에 지대한 영향을 미친다. 특히 구멍이 물체 내부에 존재하거나 꺾어지는 부분 등이 존재하면 이러한 영역에서 물체는 특이(singular)한 거동을 나타낸다. 예를 들어, 동력을 전달하는 기어 축에 기어를 조립하기 위하여 핀(pin) 구멍을 형성하였을 경우, 이 핀 구멍 근처에는 응력집중(stress concentration) 현상이 발생한다. 또한 물체가 예리하게 꺾어져 있는 코너(corner)부나 균열(crack)과 같이 예리한 틈이 존재하는 영역 등에서도 주위와 비교하여 엄청나게 큰 응력(stress)값을 나타낸다.
이렇게 물체의 거동에 특이성을 유발하는 물체의 특수한 형상을 특징 형상이라고 부르고, 유한요소 해석에 있어 해석 결과의 정확성을 확보하기 위해 주의를 기울여야 한다. 보편적으로 특징 형상을 가진 물체영역에는 매우 작은 요소 크기(element size)로 요소망(mesh)을 생성하여야 한다. 그리고 특징 형상 부위로 갈수록 조밀한 요소망이 되도록 편향 요소망(gradient mesh)을 적용하는 것이 해석 결과의 정확성과 해석 시간의 효율성 측면에서 대단히 효과적이다.
.
막대 형상을 지닌 구조물(beam-like structure)의 횡방향 처짐에 관한 거동을 모사하기 위한 공학적 이론들은 이미 오래 전부터 연구되어 왔다. 그 중에서 가장 기초가 되는 이론은 오일러 보(Euler beam) 이론은 부재 내 두께방향으로의 횡전단 변형(transverse shear deformation)을 무시하고 단순히 굽힘에 의한 변형만을 반영하고 있다.
하지만 부재의 길이에 대한 상대적인 두께비가 증가할수록 두께 방향으로의 전단 변형은 증가하기 때문에 오일러 보 이론의 정확성은 감소한다. 따라서 이러한 단점을 보완하기 위한 보 이론이 바로 티모센코 보 이론으로서, 러시아 출신 응용역학자인 티모센코(Timoshenko, 1878-1972)에 의하여 최초로 제안되었다.
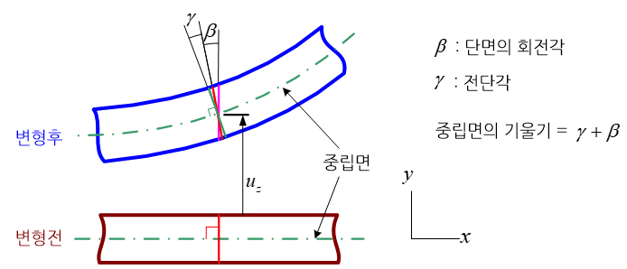
티모센코 보 이론에서는 보의 처짐과 보의 기울기를 미지수로 하고 있으며, 그 결과 티모센코 보 요소는 한 절점(node)에서 처짐과 보의 기울기를 자유도(degree of freedom)로 가지고 있다. 참고로, 횡 전단 변형률을 무시한 오일러 보에서는 보의 기울기와 단면의 기울어짐 각도가 같다고 가정하고 있기 때문에 모의 기울기를 별도의 미지수로 가지지 않는다.
.
물체 변형의 크기를 나타내는 변형률(strain)에는 탄성 변형률과 소성 변형률(plastic strain)이 선형적으로 결합되어 있다. 전자는 물체에 작용하고 있던 하중이 제거되면 함께 사라져 물체를 초기 형상으로 복원시키고자 한다. 반면 후자는 하중을 제거하여도 여전히 남게 되어 물체가 영구적으로 변형된 형상을 유지하도록 한다.
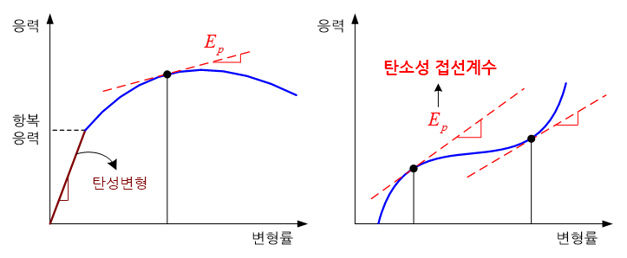
하중의 크기가 항복응력(yield stress)을 초과하지 않을 정도로 작은 경우에는 탄성 변형률만 존재하게 되지만, 항복응력을 초과하게 되면 소성 변형률도 함께 발생하게 된다. 이와 같이 항복응력을 초과한 물체의 변형을 소성변형 영역에 있다고 하며, 응력-변형률 선도(stress-strain diagram)는 직선이 아닌 곡선 형태로 표현된다. 변형이 탄성영역 내에 있을 경우에는 응력과 변형률은 선형적인 관계를 나타내며 응력-변형률 선도의 기울기는 변형률의 값과는 무관하게 항상 일정한 값을 가지게 된다. 이 기울기를 탄성계수(elastic modulus) 혹은 영률(Young’s modulus)이라고 부른다.
하지만 소성변형 영역에서는 탄성계수를 사용하지 않고 선도의 접선 기울기로 물체의 강성을 표현한다. 그리고 이 기울기는 변형률의 크기에 따라 변하는 값으로 이 기울기를 특별히 탄소성 접선계수로 정의하고 있다.
.
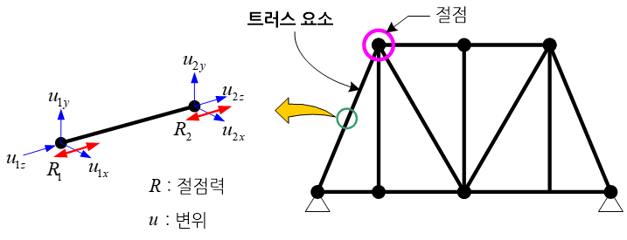
트러스는 고층건물 내부의 기본골격을 이루는 강철 구조나 각종 교량이나 타워 및 소형 선반에 이르기 까지 우리 생활과 밀접한 부재이다. 이러한 트러스 구조물은 각 부재의 양 끝단을 볼트나 핀 등을 통하여 결합되어 있다. 역학적인 측면에서 이러한 트러스 구조물은 외부 하중에 대하여 구성 요소 하나 하나가 단지 인장력이나 압축력만을 지탱한다. 이러한 측면에서 트러스 부재는 이력 부재(two-force member)에 해당된다.
트러스 구조물의 역학적 거동을 유한요소해석(finite element analysis)과 같은 수치기법(numerical technique)으로 분석하기 위해 사용되는 추상적인 부재(혹은 유한요소 모델)를 트러스 요소라고 부른다. 여기서 추상적이라는 용어는 3차원 형상을 지닌 트러스 부재를 중립축(neutral axis)과 같은 부재의 중심축을 따라 하나의 선으로 그 형상을 간략화 시키고, 이 간략화 된 1차원 형상에 대하여 역학적 모델식이 유도됨을 의미한다.
따라서 실제 수치해석에서 트러스 구조물은 선요소(line element)들로 요소망(mesh)이 구성되며, 상세한 단면정보(단면형상, 단면적, 면적 관성 모멘트(area moment of inertia) 등)는 입력창을 통하여 해석자가 입력하도록 되어 있다. 이렇게 입력된 단면정보는 트러스 구조물에 대한 강성행렬(stiffness matrix)과 질량행렬(mass matrix) 계산에 사용된다. 그리고 하나의 트러스 요소의 양 끝점에 절점(node)이 할당되며, 하나의 절점에는 세 개의 병진 자유도가 부여되어 있다.
.
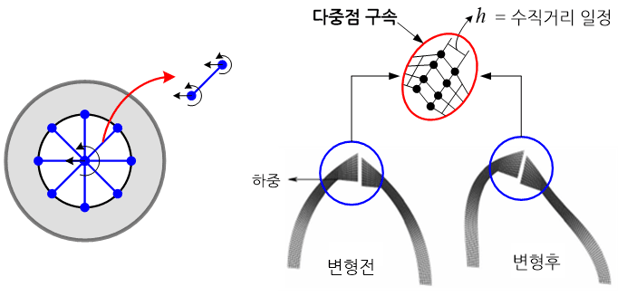
한 물체의 거동이 주위에 고정 혹은 움직이는 다른 물체와 구속관계를 가지고 있는 문제를 유한요소해석(finite element analysis)으로 시뮬레이션 하기 위해 필요한 특수한 유형의 수치기법이다. 유한요소 해석을 위해 대상이 되는 물체를 여러 개의 요소로 세분화 시키고 주위 물체와 실제로 구속되는 한 점 혹은 국부영역 내 절점(node)들을 구속관계에 있는 물체의 해당 절점들과 구속관계를 유지하도록 연결시키는 역할을 한다. 강체요소(rigid element)로 통칭하여 불리기도 하는데 차이점은 다수의 강체요소들을 이용하여 구속관계에 있는 절점들을 연관시키는 수치기법이라는 점이다.
다중점 구속은 접촉 경계에서 요소망(mesh)이 서로 일치하지 않는 경우, 두 요소망을 손쉽게 결합시키기 위해 사용되는 것 외에도 다양한 용도로 활용되고 있다. 예를 들어 자동차 타어어의 회전중심에 병진속도 혹은 각속도를 부여해야 할 경우, 회전중심과 타이어 내측 원주면 상의 점절들을 다수의 강체요소로 연결하여 원하는 속도 구속조건을 부과할 수 있다.
그리고 한 물체 내 일부 형상의 동적인 효과만을 간략하게 반영하고자 할 경우, 일부형상의 관성효과를 집중질량(lumped mass)으로 모델링하고 이 질중질량을 요소망으로 실제 표현된 나머지 물체 형상에 연결시킬 수 있다. 이와 같이 다중점 구속은 비접합 요소망(incompatible mesh) 사이의 결합, 접촉해석(contact analysis)에서의 각종 접촉조건 구현, 집중질량 처리, 요소망 외부에 부여되어 있는 각종 구속조건 처리 등을 위해 매우 효과적으로 사용되고 있다.
.
그라스호프 수는 유체에 작용하는 부력과 점성력의 비로 정의되는 무차원 수이다. 열팽창과 중력의 영향으로 야기되는 자연대류의 특성을 나타내는 무차원 수이다.
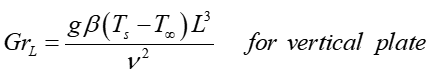
, where g: 중력가속도, β: 열팽창계수(thermal expansion coefficient),, Ts: 표면 온도, T∞: 유체온도, ν: 동점성(kinematic viscosity), L: 특성길이(characteristics length)
해석 정확도를 높이고, 반복 작업을 줄여보세요.
내게 맞는 솔루션 찾기