
설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
통합검색


Search Close

설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
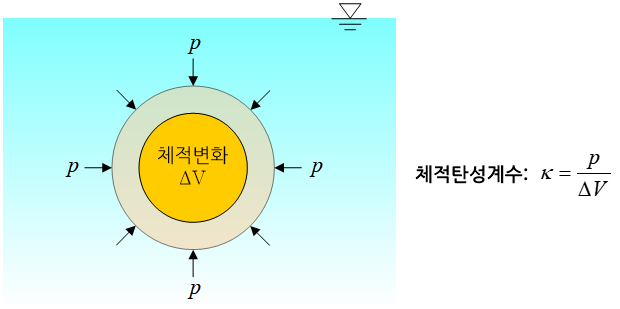
물체의 부피변화에 저항하려는 강성(stiffness)을 특별히 그 물체의 체적 탄성계수라고 부른다. 고무풍선을 물 속에 넣으면 눈으로 관찰할 수 있을 만큼 그 부피가 줄어들지만 금속과 같은 재질로 만든 물체를 물 속에 넣으면 부피의 변화를 거의 관찰하기 힘들다. 이것은 고무풍선을 내부에 채워져 있는 공기의 체적 탄성계수가 금속의 체적 탄성계수보다 낮기 때문이다.
임의 물체의 체적 탄성계수는 역학적으로 그 물체의 체적변화로 그 물체에 작용하는 정수압(hydrodynamic pressure)을 나눈 상대비로 정의된다. 따라서 체적 탄성계수는 [하중]/[면적]의 단위(unit)를 가진다. 만일 물체가 부피 변화가 전혀 없는 비압축성(incompressible) 물체라고 한다면 이 물체의 체적 탄성계수는 무한대이다. 대표적인 비압축성 물질로 고무를 들 수가 있다.
이러한 비압축성 물질의 거동을 유한요소법(finite element method)으로 해석하는 경우, 잠김현상(locking phenomenon)이라 불리는 수치해석 상의 특수성으로 해석의 정확도를 확보하기가 대단히 어렵다. 이것을 해결하기 위해 몇 가지 특수한 수치기법(numerical technique)들이 소개되어 있는데, 가장 대표적인 기법으로 벌칙기법(penalty method), 라그랑지 승수법(Lagrange multiplier method), 그리고 u-p 혼합기법(u-p mixed method) 등이 있다.
.
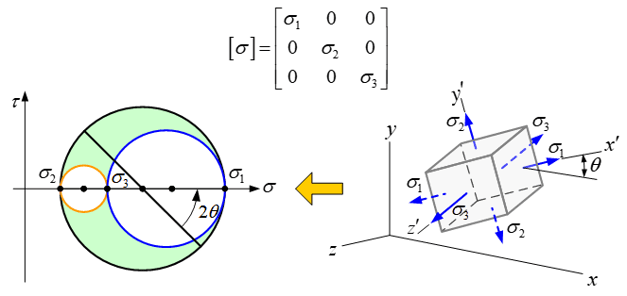
물체가 외부로부터 힘이나 모멘트를 받으면 물체 내부에는 저항하려는 힘이 발생한다. 그리고 이 물체 내부의 저항력을 해당 지점의 단위 면적으로 나눈 값을 응력(stress)으로 정의한다. 힘은 크기뿐만 아니라 방향을 가지고 있기 때문에 응력 또한 크기와 방향성을 지니고 있다.
따라서, 물체 내부 임의 한 점에 있어서 응력의 크기는 응력 계산의 기준이 되는 좌표축의 방향에 따라 변한다. 좌표축의 방향에 따른 응력값의 변화는 모어 원도(Mohr’s circle)를 통해 한 눈에 쉽게 파악할 수 있다. 2차원의 경우 좌표축은 두 개의 직교하는 축을 가지기 때문에 한 방향이 최대 응력값을 나타내면 직각이 되는 다른 한 방향은 최소 응력값을 나타낸다. 3차원의 경우에 좌표축은 세 방향을 가지므로 한 방향이 최대 응력값을 가질 경우, 나머지 두 방향은 각각 최소 응력값 및 중앙 응력값을 가지게 된다.
이와 같이 최대, 최소 및 중앙 응력값을 주 응력이라고 부르고, 주 응력값을 가지는 좌표축의 방향을 주축(principal axes)이라고 정의한다. 주 응력과 주축은 물체의 강도분석에 있어 대단히 중요한 역할을 한다. 왜냐하면 물체의 파괴는 물체 내 응력의 최대값에 직접적으로 좌우되기 때문이다. 주 응력이나 주축의 개념은 변형률(strain), 질량 관성모멘트(mass moment of inertia) 및 면적 관성모멘트(area moment of inertia)의 좌표축에 따른 특성에도 그대로 적용된다.
.
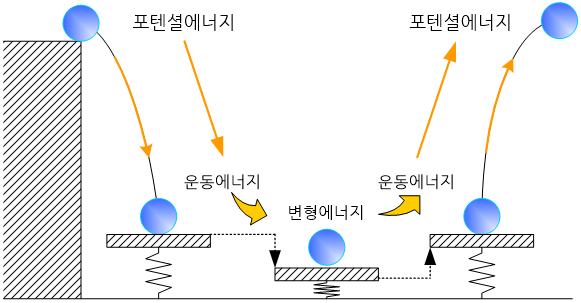
에너지는 일(work)을 할 수 있는 능력을 의미하고, 일과 동일한 물리적 단위(unit)를 지니고 있다. 고속도로를 질주하는 자동차는 다른 물체와 부딪혔을 때 차체를 찌그러뜨릴 수 있는 운동에너지(kinetic energy)를 가지고 있고, 옥상에 놓여 있는 물체는 지면에 떨어졌을 때 지면에 충격하중(impulse force)을 가해 변형시킬 수 있는 위치 에너지(position energy)를 가지고 있다. 이 외에 우리 주위에는 화력, 수력, 풍력 등과 같은 다양한 에너지 원(energy source)이 존재한다.
에너지 중에서 일로서 외부로 소모되지 않고 보존되는 에너지를 특별히 포텐셜 에너지라고 부른다. 엄밀한 의미에서 지구상에는 일로 전혀 소모되지 않는 순수한 포텐셜 에너지를 가지는 물체는 존재하지 않는다. 예를 들어 구슬을 지면에 떨어뜨리면 지면에 부딪힌 후 다시 튀어올라 원래 높이까지 올라와야 하지만 조금 낮은 위치까지만 상승한다. 그 이유는 위치 에너지의 일부가 구슬과 공기와의 마찰에 따른 마찰일과 지면을 변형시키는 일로 소모되기 때문이다. 따라서, 이렇게 외부로 소모되는 일이 존재하는 경우에 있어서 포텐셜 에너지는 전체 에너지 중에서 외부로 소모되는 일만큼 뺀 나머지 에너지로 정의된다.
포텐셜 에너지는 공학분야에 있어 대단히 중요한 역할을 하며, 특히 최소 포텐셜에너지 원리(minimum potential energy theorem)는 물체의 거동을 분석하는 근간이 될뿐더러, 레일레이-리쯔 방법(Rayleigh-Ritz method)과 같은 수치기법의 토대가 된다.
다공성 매질(Porous media)은 필터, 유동 분배기 등과 같이 유동의 압력손실 또는 방향 변화를 유발하는 유동해석영역 내부의 특수한 성질이다. 이러한 성질을 가진 얇은 판을 일반적으로 타공판이라고 부른다. 타공판을 실제로 모델링 하기 위해서는 모델 내부에 많은 구멍을 만들어 모델링 해야 하는데, 이는 모델링이 매우 어렵고, 모델링이 가능 하더라도 해석 비용이 지나치게 많이 들어 해석이 어려운 문제점이 있다.
CFD에서는 다공성 매질의 특징을 표현 하면서, 위의 문제점을 해결 하기 위해 타공판 경계 조건을 이용하여 모델링을 간략화 하고, 적은 해석 비용으로 타공판에 대한 해석을 진행할 수 있다. 타공판 경계조건은 일반적으로 다공성 매질의 해석에 사용되는 점성저항, 관성저항을 이용하여, 속도에 따른 압력 손실을 적용하는 경계 조건이다. 타공판의 특징은 저항곡선(resistance curve)로 표현하며, 일반적으로 타공판의 저항 곡선은 속도가 증가함에 따라 압력손실이 커진다.
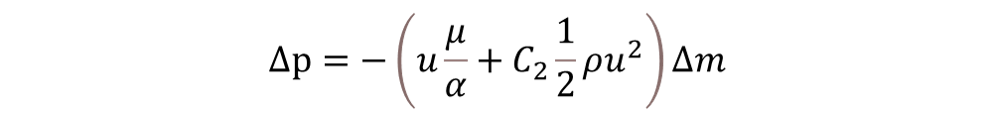
: 투과율
: 점성 저항
: 관성 저항
: 타공판 두께
물체의 량이 시간과 더불어 증가하다가 일정한 값으로 접근하는 거동을 포화(saturation)된다고 하고, 시간과 더불어 감소하다가 일정한 값으로 접근하는 거동을 쇠퇴(decay)한다고 말한다.
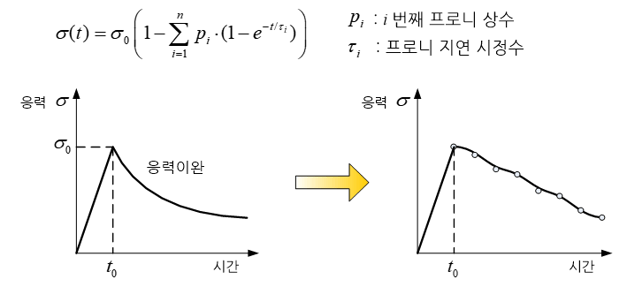
프로니 급수는 후자와 같은 물체의 거동을 수치적으로 근사화 시키기 위해 사용되는 급수이다. 이 급수는 크기가 순차적으로 변하는 시간함수(time function) (혹은 시간상수(time constant)를 가진 유한개의 지수함수들의 조합으로 표현되는 시간에 대한 급수 함수(series function)로 정의된다. 그리고 각각의 지수함수에 곱해WL는 미지의 상수는 대상이 되는 물체의 실제 쇠퇴거동으로부터 결정된다. 프로니 급수는 고무와 같이 점탄성(viscoelasticity)을 지닌 물체의 시간에 따른 응력이완(stress relaxation) 현상을 수치적으로 근사화 하기 위해 효과적으로 사용되고 있다.
하중을 받아 물체 내부에 발생하는 응력(stress)이 하중제거와 더불어 지수함수적으로 감소하는 현상을 응력이완이라고 부르고, 이러한 물체의 거동은 물체의 점탄성(viscoelasticity)에 기인한다. 하중을 제거한 후 응력이 시간과 더불어 감소하는 거동을 프로니 급수를 이용하여 근사화 시키기 위해서는, 해당 물체의 시편을 이용하여 측정한 응력이완 실험 데이터로부터 각각의 지수함수에 곱해지는 재료상수라 불리는 계수를 결정해야 한다. 실험 데이터로부터 이들 계수를 결정하기 위해서는 일반적으로 최소자승법(least square method)을 적용하고 있다.
.
스프링에 힘을 가해 잡아당기면 길이 방향으로 늘어나게 되는데, 늘어나는 길이는 가해진 힘의 크기와 스프링 상수(spring constant)에 의해 결정된다. 만일 늘어난 길이가 힘에 비례하고 스프링 상수에 반비례 관계에 있다면 이 스프링은 선형(linear)적인 거동을 나타낸다고 할 수 있다. 하지만 힘의 크기에 비례하지 않고 스프링 상수에 반비례적인 관계에 있지 않다면 스프링은 비선형(nonlinear)적 거동을 나타낸다고 말할 수 있다.
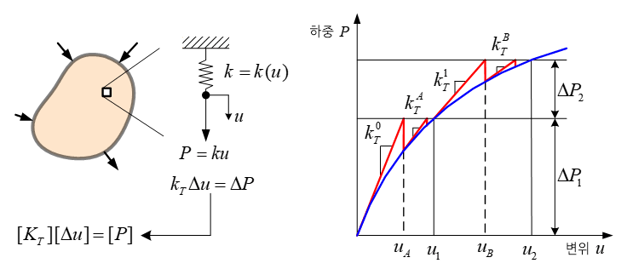
이러한 개념은 유한한 체적을 가진 일반적인 탄성체(elastic body)에도 그대로 적용된다. 선형해석(linear analysis)에서는 물체의 변형(deformation)은 외부 하중에 대해 선형적인 관계를 나타내기 때문에, 강성행렬(stiffness)은 일정한 값을 유지한다. 하지만, 물체의 변형이 외부 하중에 대해 비선형적인 거동을 나타내는 비선형 해석(nonlinear analysis)에 있어서 강성행렬은 일정한 값이 아니라 물체 거동의 크기에 따라 계속해서 변한다. 따라서 비선형 해석에 있어서는 이렇게 물체 거동에 따라 변하는 물체의 강성행렬을 계속적으로 갱신해야 하는 번잡한 계산과정이 필요하다.
물체의 거동에 따라 변하는 물체의 강성을 정의하는 하나의 방법으로 접선계수(tangent stiffness)라는 것이 있다. 이것은 용어 그 자체가 의미하듯이 물체의 거동값에 해당하는 물체의 강성을 물체 거동 곡선의 접선으로 정의하는 방법이다. 유한요소 해석(finite element analysis)에 있어서 이러한 접선은 행렬 방정식으로 전환하였을 때, 하나의 행렬로 표현되며 이 행렬을 접선계수 행렬이라고 부른다.
그리고 이 접선계수 행렬은 비선형 해석을 위해 주로 사용되는 뉴튼-랩슨 기법(Newton-Raphson method)과 같은 반복계산 기법에 있어 물체 거동의 증분(increment)을 계산하기 위해 사용된다.
.
정상상태란 어떤 물리적 상태를 나타내는 밀도, 압력, 온도, 속도 등의 값이 시간에 따른 변화가 없음을 의미한다. 정상상태에 반대되는 말로 과도상태(transient) 혹은 비정상상태를 사용한다.
보통 유동해석에서의 정상상태란 유동장이 시간에 따른 변화가 없음을 의미하며 유동이 안정된 상태를 의미한다. 열역학적인 관점으로 살펴보면 어떤 계에 물리량의 출입이 있는 상태에서 그 계의 물리적 상태가 어떤 공간에서도 시간적으로 변하지 않음을 의미한다.
유동해석과 관련된 방정식인 Navier-Stokes 방정식에는 시간과 관련된 항이 있는데 이 항은 시간에 따른 물리량의 변화율을 의미한다. 정상상태는 시간에 따른 물리량에 변화가 없음을 의미하므로 정상상태에서는 이 시간항이 0을 의미한다. 유동이 난류의 특성을 나타낼 경우 유동은 불규칙적인 소용돌이가 나타나게 되는데 이 경우 계속해서 유동에 변화가 생긴다. 이런 경우에는 앙상블 평균을 통해 유동의 움직임이 평균적으로 일정하게 나타날 경우 정상상태라고 하기도 한다.
물과 같은 유체 흐름에 대한 유동해석(flow analysis)은 유체로 가득찬 영역을 대상으로 하는 경우와 그렇지 않은 경우로 구분할 수 있다. 유체로 가득찬 유동을 대상으로 하는 경우에는 유체로 채워져 있는 영역과 그렇지 않은 영역을 구분할 필요가 없다. 하지만 유체가 부분적으로 채워져 있는 경우에는 유체로 채워져 있지 않는 영역과의 경계를 구분해야 한다.
이러한 경계가 유동과 무관하게 공간상에 항상 고정되어 있다면 문제는 간단하지만, 그렇지 않고 유동과 더불어 항상 변하는 경우는 그리 간단하지가 않다. 자유표면이란 유체 유동이 공기와 접하는 상층 표면을 의미한다. 라그랑지 기술법(Lagrange description)의 유한요소법을 이용하는 경우에는 유한요소(finite element)가 유동과 동일한 속도로 공간상에서 이동하기 때문에 자유표면은 자동적으로 정의된다. 하지만 오일러 기술법(Euler description)의 유한체적법(finite volume method)에서는 그리드 격자가 공간상에 고정되어 있기 때문에 자유표면을 파악하기 위해 특별한 알고리듬이 요구된다.
가장 보편적인 방법으로는 각각의 그리드 격자 내에 포함된 유체량을 그리드 체적에 대한 상대비율인 체적분율(volume fraction)을 이용하는 것이다. 이것을 이용하면 자유표면을 포함하는 그리드 격자의 체적분율은 0과 100%의 사이의 값을 가지게 되고, 이러한 값을 나타내는 인접한 그리드 격자들의 좌표값에 보간법(interpolation)을 적절히 적용하면 자유표면을 정의할 수 있다.
또 다른 수치기법으로는 자유표면 근처에는 라그랑지 기술법을 그리고 나머지 유체 영역에는 오일러 기술법을 혼합한 에이엘이 기술법(ALE description)을 적용하는 것이다.
.
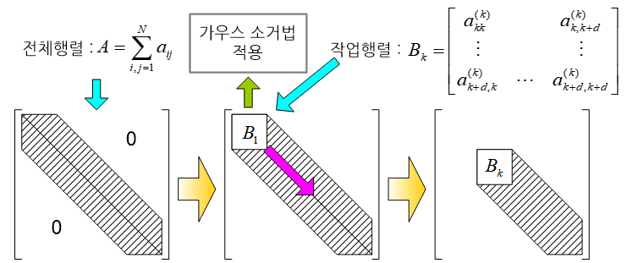
임의 물체의 거동을 유한요소법(finite element method)으로 근사화시키면 물체의 강성은 강성행렬(stiffness matrix)로 그리고 관성력(inertia force)은 질량행렬(mass matrix)로 표현된다. 그런데 이러한 행렬의 크기는 요소망(mesh)의 크기에 비례하여 증가하기 때문에, 대형 해석문제로 갈수록 행렬이 커져서 컴퓨터에 저장해야 할 행렬요소가 기하급수적으로 증가하게 된다.
그럼에도 불구하고 일반 개인용 컴퓨터로도 대형 해석문제를 수행할 수 있는 이유는 무엇일까? 그 이유는 유한요소법을 통해 만들어지는 강성행렬과 질량행렬이 띠형상의 분산행렬(banded sparse matrix)이라는 특성때문이다. 행렬의 대각선 주위에만 0이 아닌 행렬요소가 밀집되어 있기 때문에 행렬 전체를 저장하지 않고서도 행렬연산을 수행할 수 있기 때문이다.
이와 같이 행렬 전체를 저장하지 않고 행렬의 대각선을 따라 0인 아닌 행렬의 일부 영역만을 순차적으로 저장해 나가면서 행렬방정식을 풀어나가는 알고리듬이 바로 프론탈 솔버이다. 구조강도 해석과 같은 선형 정적(linear static) 해석은 거의 대부분 이 솔버를 적용하고 있으며, 최근 멀티 프론탈 솔버(multi-frontal solver)와 병렬연산(parallel computing)의 등장으로 저용량 컴퓨터로도 초대형 문제를 아주 빠른 시간내에 해석할 수 있게 되었다.
이 솔버를 프론탈 솔버라고 부르게 된 것은 대각선을 따라 0이 아닌 행렬요소들을 순차적으로 저장하여 풀어나가는 것이 마치 파도가 밀려오는 양상과 흡사하기 때문이다.
.
해석 정확도를 높이고, 반복 작업을 줄여보세요.
내게 맞는 솔루션 찾기