
설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
통합검색


Search Close

설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
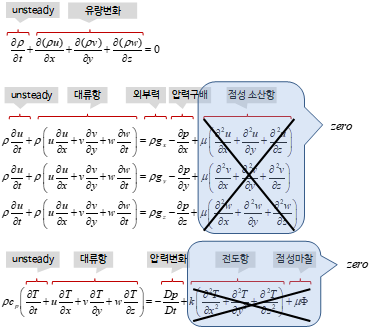
오일러 방정식은 단열 비점성 유동(adiabatic & inviscid flow)에 적용 가능한 방정식이다. 나비어-스톡스 방정식에서 점성항과 전도항이 없는 경우에 해당한다. 때로는 오일러 방정식이 연속방정식과 에너지 방정식을 포함한 비점성 유동의 전체 지배 방정식을 뜻하기도 한다.
l 질량보존의 법칙: 연속방정식(continuity equation)
l 운동량보존의 법칙: 오일러 방정식(Euler equations)
l 에너지보존의 법칙: 에너지 방정식(energy equation)
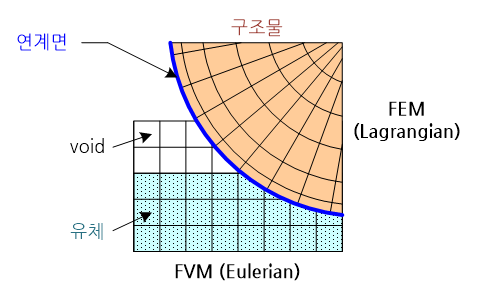
유체와 구조물이 접촉하고 있는 경우 유체의 유동과 구조물의 변형(deformation)은 두 매질의 공통경계(common interface)를 통하여 상호 영향을 미친다. 이러한 유체-구조 연계해석(fluid-structure interaction analysis)에 있어 구조물은 라그랑지 기술법(Lagrange description)의 유한요소법을 그리고 유체 영역은 오일러 기술법(Euler description)의 유한체적법(finite volume method)을 주로 사용하고 있다.
그 주된 이유는 구조물은 연속체(continuum body)로써 변형의 정도가 유체에 비하여 비교가 되지 않을 정도로 작아서 변형에 따른 요소망(mesh)의 찌그러짐이 그다지 문제가 되지 않는다. 하지만, 유체는 흐름이 매우 복잡하고 혼동스럽기 때문에 라그랑지 기반의 요소망을 적용하게 되면 요소의 찌그러짐이 큰 문제로 대두된다. 따라서 유체 영역은 유체의 흐름과는 무관하게 항상 공간상에 고정된 오일러 기반의 격자를 적용하게 된다.
이와 같이 움직이는 요소망과 공간상에 고정된 격자 사이 공통경계에서, 요소망과 격자의 분포가 정확히 일치하지 않는 경우에 유체의 압력과 구조물의 변형을 서로 주고 받기 위한 연계처리기법이 바로 오일러-라그랑지 연계법이다. 이 기법은 에이엘이 연계법(ALE coupling)과는 달리 두 매질이 접촉하고 있는 공통경계의 기하학적 형상이 복잡한 경우에 매우 효과적이다.
그 이유는 구조물의 요소망과 유체의 격자 중에서 조밀한 경계면을 단순히 연계요소망(coupling mesh)로 정의하기만 하면 되기 때문이다. 이러한 장점 때문에 거의 대부분의 유체-구조 연계해석에서는 이 연계법을 적용하고 있다. 그 대표적인 경우로 자동차 타이어의 수막현상(hydroplaning) 그리고 선박의 유탄성(hydroelasticity) 해석을 들 수 있다.
.
물체에 힘을 가하면 그 내부에는 힘의 크기에 상당하는 응력(stress)이 발생한다. 역학적인 측면에서 응력은 물체 변형의 정도를 나타내는 변형률(strain)의 크기와 상관관계를 맺고 있으며, 이 상관관계는 물체의 재료 물성치(material property)를 통해 표현된다.
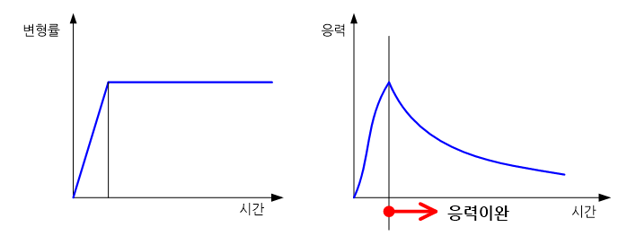
응력이완이라 함은 물체에 힘을 가하여 그 상태를 유지하고 있더라도 물체 내부의 응력이 시간과 더불어 감소하는 거동을 의미한다. 응력이완은 소성변형(plastic deformation) 된 물체가 하중을 제거하면 탄성에 해당하는 응력성분이 제거되면서 변형량이 다소 감소하는 스프링 백(spring-back)과는 뚜렷한 차이를 나타낸다. 그리고 하중 즉 응력이 일정하게 유지되더라도 변형률이 시간과 더불어 지속적으로 증가하는 크리프 현상(creep phenomenon)과도 구별되는 거동이다.
응력이완은 고무나 콘크리트와 같이 점탄성(viscoelasticity) 혹은 점탄소성(visco-elastoplasticity)을 지니는 재료에서 발견할 수 있는 거동으로 탄성영역에서의 응력이완과 소성영역에서의 응력이완으로 구분할 수 있다. 전자의 경우는 물체 내 응력이 탄성범위에서 이완되는 반면 후자는 소성범위에서의 응력이 감소하는 거동을 일컫는다. 응력이완에 대한 수치해석은 매우 난해하기 때문에 해당 재료의 응력-변형률 선도(stress-strain diagram)의 시간에 따른 변화를 실험적으로 측정하여 근사적으로 계산하는 방법이 많이 사용되고 있다. 시간함수로 표현되는 프로니 급수(Prony series)를 이용한 근사기법이 대표적인 예이다.
.
연속체 가정(continuum assumption)과 뉴턴유체(Newtonian fluid) 가정을 만족하는 유체의 지배방정식은 다음과 같다.
l 미지수: 밀도(ρ), 속도(u, v, w), 압력(p), 온도(T)
l 질량보존의 법칙: 연속방정식(continuity equation)
l
운동량보존의 법칙: 나비어-스톡스 방정식(Navier-Stokes equations)
l
에너지보존의 법칙: 에너지 방정식(energy equation)
l
이상기체 법칙: 상태방정식(equation of state)
위 6개의 방정식으로 6개의 미지수(ρ, u, v, w, p, T)를 구할 수 있으며, 이 방정식들이 유체역학의 근간이 되는 지배방정식이다.
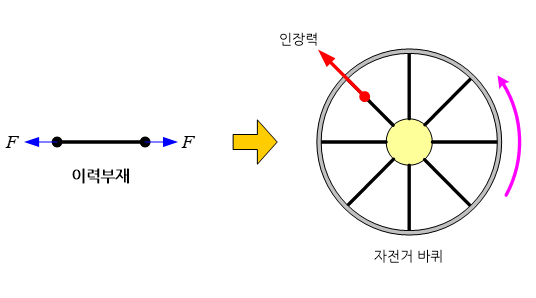
이력(two-force)이라는 용어가 암시하듯이 한 물체에 두 개의 힘만이 작용하는 부재로서, 한 물체를 서로 다른 두 지점에서 힘을 가하여 잡아 당기는 경우를 생각해 보자. 두 힘의 방향은 두 지점을 연결하는 직선의 연장선 상에 놓이게 될 것이다. 이러한 하중을 받는 부재를 공학에서 이력 부재라고 부른다.
이력 부재의 대표적인 예로는 자전거의 휠과 축을 연결하는 다수의 강선(steel wire)을 들 수 있다. 이 강선은 휠과 축으로부터 인장력 만을 받게 된다. 또한 서로 다른 부품을 연결하는 각종 링크(link)도 이력 부재의 전형적인 예이다. 이력 부재는 모멘트를 지탱하지 못하고 단지 인장 혹은 압축하중만을 지탱하기 때문에 유한요소 해석에서 일반적으로 링크 요소(link element)로 모델링 된다.
.
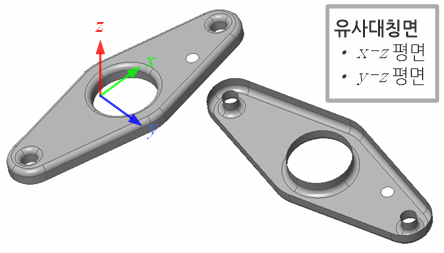
임의 자연현상이나 물체의 거동이 특정한 선, 면 혹은 축을 중심으로 대칭이 되는 경우를 대칭문제(symmetric problem)라고 부른다. 대칭에는 완전 대칭과 유사 대칭으로 구분할 수 있다. 전자는 물체의 형상, 재질, 하중상태 및 구속조건이 완전히 대칭이 되는 경우를 말한다.
하지만, 이러한 완전 대칭 조건을 만족하지는 않지만 거의 유사하게 대칭이 되는 경우를 종종 발견할 수 있다. 예를 들어, 위에서 언급한 대칭 조건의 요구사항들 중에서 일부가 대칭성을 조금 이탈한 경우가 이에 해당된다.
재질, 하중상태 및 구속조건이 완전히 대칭을 이루지만 형상적인 측면에서 한 쪽에는 작은 구멍을 가지고 있는 반면 다른 한 쪽에는 구멍이 없는 경우를 생각해 보자. 이러한 경우, 구멍이 있는 쪽이 구조적으로 취약하다. 따라서 구멍이 없는 쪽에 동일하게 구멍이 있다고 가정하여 대칭문제로 취급하여도 무방하다. 왜냐하면, 원래 형상보다 대칭으로 가정한 형상이 구조적으로 강도가 낮기 때문에 안전율(safety) 측면에서 보다 안전한 설계에 이르게 한다.
이와 같이 우리 주위에는 유사 대칭을 나타내는 문제를 많이 발견할 수 있으며, 완전 대칭으로 가정하여 해석을 효과적으로 수행할 수 있다. 하지만 이렇게 유사 대칭을 완전 대칭으로 가정할 경우, 유념해야 할 사항은 완전 대칭으로 가정한 문제가 원래 문제보다 안전한 설계를 보장할 수 있어야 한다는 점이다.
한편, 대칭성에서 이탈한 정도가 아무리 미미 하더러도 완전 대칭으로 가정하여 풀 수 없는 문제들도 있다. 예를 들어, 완전 대칭성을 깨뜨리는 사항이 물체 거동에 지배적인 인자라고 한다면 완전 대칭으로 가정하여 풀게 되면 전혀 다른 해답에 도달할 수 있기 때문이다.
.
임의 자연현상을 유한요소해석(finite element analysis)과 같은 시뮬레이션을 통하여 해답을 구하게 되면 이 해답은 정담이 아니라 근사해(approximate solution)이다. 따라서 반드시 정답과의 차이, 즉 오차(error)가 발생하게 된다.
이 오차를 줄이기 위해서는 문제 영역을 세분화 시킨 유한요소(finite element)의 개수를 증가시키거나 보간함수(interpolation function)의 차수를 증가시켜야 한다. 해가 특이성(singularity)을 나타내는 영역에는 전자가 효과적이며, 그렇지 않고 해가 완만한 변화를 보이는 영역에는 후자자 효과적인 것으로 알려져 있다.
대부분의 경우, 목표로 하는 정확도를 가지는 근사해를 구하기 위해 필요한 요소의 개수나 기저함수(basis function)의 차수는 해석결과를 구하기 전에는 알 수 없다. 따라서 해석을 수행하기 전에 문제영역 전체를 동일한 보간함수 차수를 가진 유한요소들로 균일하게 세분화 한다. 그런 다음 필요에 따라 오차평가(error estimate)를 수행하고 이 오차정보에 따라 필요한 영역에 유한요소 개수를 증가시키거나 기저함수의 차수를 높이게 된다.
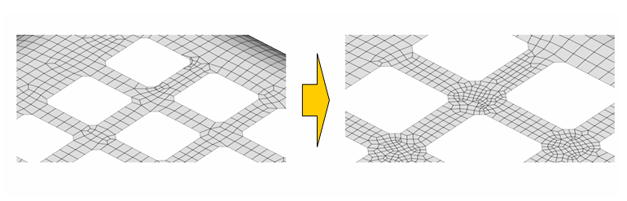
이렇게 근사해의 정확도를 향상시키기 위하여 유한요소의 개수를 증가시키는 것을 요소망 세밀화라고 부른다. 참고로 일정한 크기의 문제 영역 내에 유한요소의 개수를 증가시킨다는 것은 결국 유한요소의 크기를 줄이는 것이다. 요소망 세밀화는 문제 영역 전체에 걸쳐 수행할 수도 있고, 오차가 높은 국부 영역에만 한정하여 수행할 수도 있다. 하지만 효율성 측면에서 후자의 방식이 일반적으로 사용되고 있다.
다른 한편, 초기 적용한 요소망이 너무 조밀하여 유한요소의 개수를 감소시키는 경우도 있는데, 이러한 경우를 요소망 비세밀화(mesh unrefinement)라고 부른다.
.
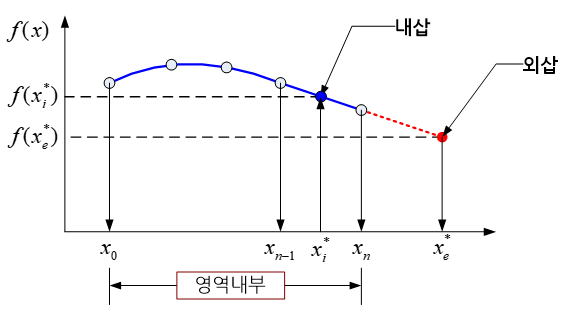
특정한 공간이나 시간 영역내 각 지점에서의 값들을 연결하면 하나의 선, 곡선 혹은 곡면이 된다. 이와 같이 특정한 구간 내 각 점에서 값들을 이용하여 연속적인 함수를 구하는 것을 보간(interpolation)이라 하고 이렇게 구한 함수를 보간함수(interpolation function)라고 부른다. 이와는 달리 특정한 구간 내에 존재하는 각 지점에서의 값들을 이용하여 이 구간 바깥에 존재하는 특정 지점까지 연속된 함수를 구하는 것을 외삽이라고 하고 이렇게 구한 함수를 외삽함수(extrapolation function)라고 부른다.
보간이나 외삽은 서로 떨어져 있는 점들에서의 값, 다시 말해 데이터(data)를 연속적인 함수로 표현한다는 점에서는 공통점을 지니고 있다. 하지만 함수로 나타내어야 할 DATA가 존재하는 영역 내부에 한정되어 있느냐 그렇지 않느냐에 따라 뚜렷한 차이점을 나타낸다. 보간이나 외삽은 실험으로 구한 각종 DATA를 연속적인 함수로 변환하고자 할 경우 주로 사용된다.
유한요소 해석(finite element analysis)에서 화면상에 출력되는 변형, 변형률(strain) 및 응력(stress)의 칼라 분포도 역시 요소망(mesh) 내 각 절점(node)에서의 값들을 보간 혹은 외삽하여 연속적인 분포로 보여주는 것이다. 보간이나 외삽을 위해서는 각 점에서의 값들을 직선으로 연결하는 가장 단순한 방법에서부터 최소자승법(least square method)에 이르기 까지 다양한 방법들이 사용되고 있다.
.
물체가 외부로부터 힘을 받을 때 저항하려는 물체 내부의 단위면적당의 힘인 응력은 물체 내부의 각 위치에 따라 변한다. 또한 한 지점에 있어서도 응력 값은 기준이 되는 좌표축의 방향에 따라 변한다. 이 것은 응력이 크기뿐만 아니라 방향을 가지는 힘을 단위면적으로 나눈 값으로 정의되기 때문이다.
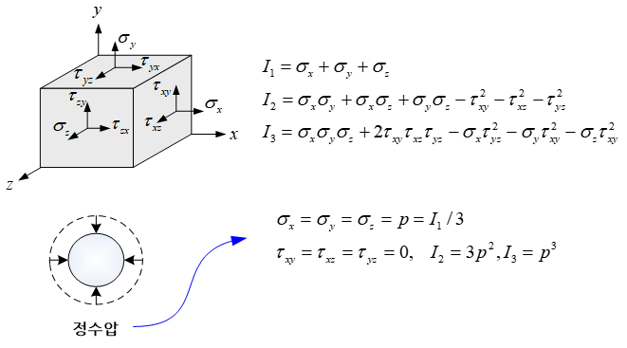
3차원의 경우, 세 축 방향으로의 수직응력(normal stress)과 서로 다른 두 축 사이의 전단응력(shear stress)의 6개로 총 9개의 응력성분이 존재한다. 수직응력 3개의 합을 제 1 응력 불변량이라고 부르며, 순수하게 물체를 압축 혹은 팽창시키는 역할을 한다. 이 외에 제 2 그리고 제 3 응력 불변량이라고 불리는 것들이 있는데, 이 것들은 물체의 영구변형(즉 소성변형(plastic deformation))을 판단하는데 주로 사용된다. 이 세 개의 값들은 설정한 좌표축의 방향과는 무관하게 물체 내 각 지점에서는 항상 일정한 값을 가지기 때문에 특별히 응력 불변량이라고 부른다.
예를 들어 물 속에 잠겨있는 공 모양의 물체가 수압을 받고 있다면, 이 물체 내부의 한 지점에서의 제 1응력 불변량은 수압과 동일하다. 그리고 이 물체는 찌그러짐이 전혀 없이 공 모양을 유지한 채 순수하게 압축만 되기 때문에 전단응력이 전혀 존재하지 않는다. 따라서 제 2 그리고 제 3 응력 불변량은 영이 되어 영구변형이 발생할 가능성은 전혀 없다. 한편, 제 1 응력 불변량은 영이고 나머지 두 응력 불변량이 존재하는 경우에는 물체가 압축되거나 팽창되지는 않고 물체형상의 찌그러짐만이 발생한다. 그 결과, 이 물체는 외부 하중의 크기에 따라 영구변형이 발생할 가능성이 높다.
.
해석 정확도를 높이고, 반복 작업을 줄여보세요.
내게 맞는 솔루션 찾기