CAE 입문자도 쉽게 이해할 수 있는 '알기 쉬운 기술 용어집'
CAE 관련 용어를 확인해 보세요.
반도체 / 디스플레이 공정 및 장비 관련 용어를 확인해 보세요.
통신 분야의 다양한 용어를 확인해 보세요.
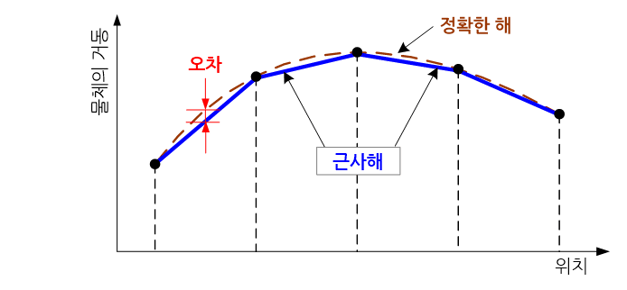
틀린 답이라고는 볼 수 없지만 정확한 답과 일치하지 않는 답을 일반적으로 근사해라고 부른다. 계산기로 1을 2로 나누면 0.5라는 값을 얻을 수 있으며 이 값은 정확한 답이다. 하지만 계산기로 1을 3으로 나누면 0.333333…이라는 값을 얻게 된다. 이 값은 틀렸다고는 볼 수 없지만 정확한 답은 아니다. 이 경우 정확한 답은 1/3이다. 하지만 이렇게 분모 및 분자로 표현하는 방식 이외에는 정확한 방법이 없다. 이 방법 외에 정확하게 표현하기 위해서는 소수점 이하 무한개의 자릿수까지 표현해야 하는데 현실적으로 불가능한 일이다. 이 것은 근사해의 단편적인 예를 보여 준다.
정답과 다른 근사해를 얻게 되는 데는 여러가지 요인이 있다. 대상이 되는 자연 현상을 수학적인 표현으로 전환시키는 과정에서 포함되는 갖가지 가정(assumption), 대상 물체의 형상을 정확하게 모델링하지 못하는 한계, 컴퓨터로 계산하는 과정에서의 계산오차 등이 대표적인 요인이다. 하나의 자연현상에 대하여 그 거동을 수치해석(numerical analysis) 기법으로 그 답을 구하게 되면, 그 답에는 두 가지의 오차(error) 성분이 반드시 포함된다. 하나는 수학적 표현으로 전환하는 과정에서 필연적으로 수반되는 가정과 형상 모델링의 한계에 따른 모델링 오차(modeling error)와 수학적 표현을 행렬 방정식으로 전환하여 컴퓨터로 계산하는 과정에서 발생하는 수치해석 오차(numerical error)이다.
따라서 자연현상에 대한 거동을 구하는 수치해석에는 오차가 필연적으로 수반되기 때문에 그 답은 정확할 수가 없다. 하지만 모델링과 계산과정이 완전히 틀리지 않는 한 이 답을 틀렸다고는 볼 수 없기 때문에 근사적으로 받아들일 수 있는 하나의 답으로 취급하고 있다.
.
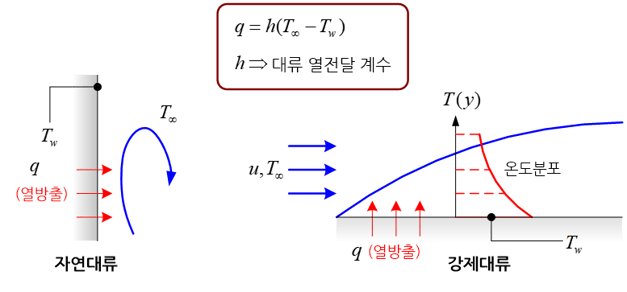
전열기 위에 찬 물이 들어 있는 주전자를 올려 놓으면 시간과 더불어 물은 가열되어 온도가 상승한다. 그리고 주전자 속에서 가열되고 있는 물을 자세히 들여다 보면 끊임없이 물이 아래에서 위로 그리고 위에서 아래로 순환되는 것을 관찰할 수 있다. 그 이유는 물의 밀도는 온도에 반비례하기 때문에 전열기와 가장 가까운 아래 쪽의 더운 물은 밀도가 낮아서 위로 상승하는 반면 상대적으로 찬 물은 밀도가 높아 아래로 하강하기 때문이다.
이와 같이 온도 차이에 의한 밀도 차이로 순환하는 유체흐름에 따란 열이 전달되는 현상을 자연대류 열전달(natural convective heat transfer)이라고 부른다. 반면, 전열기 위의 주전자를 손으로 흔들어 주게 되면 물이 가열되는데 걸리는 시간은 줄어든다. 그 이유는 온도차이에 따른 밀도차이 외에 주전자의 요동에 따라 내부 물이 강제적으로 뒤섞여서 열이 보다 잘 전달되기 때문이다. 이와 같이 유체의 강제적인 흐름에 따라 열이 전달되는 현상을 강제대류 열전달(forced convective heat transfer)이라고 부른다.
대류(convection)라는 용어 자체는 물이나 공기와 같은 유체의 흐름에 편승하여 물리량이 전달되는 현상을 지칭한다. 한편, 열의 자연대류나 강제대류 현상을 수치해석적으로 재현하기 위해서는 열전달(heat transfer)과 유동(flow)의 상호작용을 반영할 수 있는 열-유동 연계해석(thermal-flow coupled analysis) 기법을 적용하여야 한다. > 대류 열전달 더 자세히 보기🔎
열이 전달되는 방법에는 크게 전도(conduction), 대류(convection) 그리고 복사(radiation)의 세가지 유형으로 분류할 수 있다. 전도는 정지상태에 있는 고체, 액체 혹은 기체분자가 위치의 변화없이 단순히 온도차에 의해서만 열이 전달되는 형태이다. 대류는 액체나 기체 그 자체의 흐름에 편승하여 열 에너지가 전달되는 방식이다. 반면, 복사는 전자파 형식으로 열이 옮겨 가는 방식으로 진공 속을 통해서도 전달되는 특징을 지니고 있다.
대류에는 다시 자연대류(natural convection)와 강제대류(forced convection)로 세분화 되는데, 전자는 정지상태의 유체 밀도가 온도변화에 따라 달라지면서 따뜻한 유체 입자는 상대적으로 차가운 유체입자 보다 밀도가 낮아 위로 이동하면서 자연스럽게 흐름이 형성되어 열이 이동하게 된다. 하지만 후자의 경우에는 특정한 속도로 흘러가고 있는 유동 속의 유체입자가 열 에너지를 계속해서 뺏어가게 된다.
대류계수란 대류를 통해 전달되는 열에너지량의 크기를 나타내는 계수를 의미한다. 다시 말해 대류계수가 커질수록 방출 혹은 유입되는 열량은 증가하게 된다. 대류계수에는 자연 대류계수와 강제 대류계수로 구분되며, 전자는 대체로 유체의 종류에 크게 영향을 받는 반면, 후자는 유체속도 그리고 유동 방향과 물체표면이 이루는 각도 등에 따라 크게 달라진다.
.
자연계에서 발생하는 현상에 대한 근사해(approximate solution)를 구하는 대표적인 수치기법인 유한요소법(finite element method)에서는 근사해를 각 유한요소(finite element) 상에서 정의되는 보간함수(interpolation function, 혹은 기저함수(basis function))들의 조합으로 표현한다. 그리고 각 기저함수들의 크기를 결정하는 상수는 행렬 방정식을 풀어서 계산한다.
예를 들어, 구조물의 변형을 구하는 경우 행렬방정식은 [K]{u}={F}으로 표현되는데, 여기서 {u}가 바로 구해야 하는 보간함수들의 크기이다. 그리고 강성행렬(stiffness matrix) [K]와 하중벡터(load vector) {F}는 보간함수들로 근사되는 물체의 변형률 에너지(strain energy)와 하중이 한 일(work)에 비례하여 수치적분(numerical integration)을 이용하여 계산된다.
임의 물체에 대한 요소망(mesh)에 있어서 요소망 내 각 유한요소는 그 형상과 기하학적 좌표값이 각기 다르기 때문에 실제 요소 상에서 수치적분을 수행하는 것은 어려움이 많다. 그래서 컴퓨터를 이용하여 체계적으로 강성행렬과 하중벡터를 계산하기 위하여 정규화 된 마스터 요소(master element)를 활용하고 있다. 그리고 이 마스터 요소와 요소망 내 실제 유한요소 사이의 정보 교환은 좌표변환(geometry transformation)을 통하여 이루어 진다.
마스터 요소와 실제요소 사이의 좌표변환에는 자코비언(Jacobian)이 반드시 포함되어 있는데, 이것의 물리적인 의미는 1차원의 경우는 두 요소의 길이 비, 2차원의 경우는 두 요소의 면적 비 그리고 3차원의 경우에는 두 요소의 체적 비를 나타낸다. 따라서 자코비언은 물리적으로 0 혹은 음(-)의 값을 가질 수가 없다.
하지만 요소망을 생성하는 과정에서 요소가 지나치게 찌그러지게 되면 마스터 요소와의 좌표변환에 있어 0 혹은 음(-)의 자코비언을 가지게 된다. 이렇게 요소의 과도한 찌그러짐은 물리적으로 불가능한 0 혹은 음(-)의 자코비언을 야기시켜 유한요소 행렬 방정식을 풀 수 없게 만든다. 다시 말해 유한요소 해석 프로그램이 [K]{u}={F}라는 행렬방정식을 풀지 못하고 도중에 중단되어 버린다.
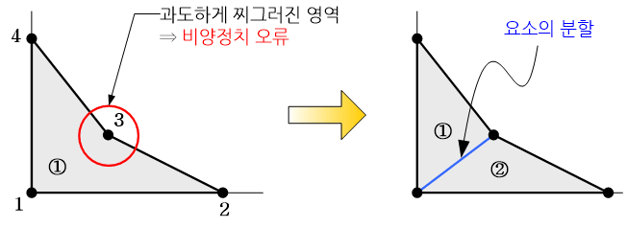
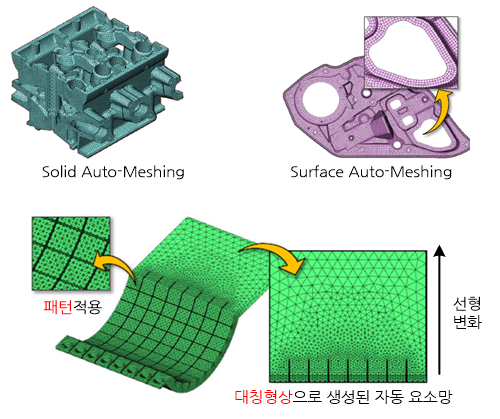
유한요소 해석(finite element analysis)을 수행하기 전에 선행되어야 할 작업들 중 하나인 요소망(mesh)은 CAE 프로그램의 자동 요소망 생성 기능을 이용하거나 혹은 해석자가 직접 생성할 수 있다. 전자를 자동 요소망 생성이라고 하고 후자를 수동 요소망(manual mesh) 생성이라고 부른다. 물체의 형상이 그다지 복잡하지 않은 경우에는 수동으로 요소망을 생성하는 것이 형상 종횡비(aspect ratio)가 높은 요소나 과도하게 찌그러진 요소(distorted element)를 예방할 수 있어 높은 정확도의 해석결과를 확보할 수 있다.
하지만 물체의 형상이 복잡한 경우에 해석자가 직접 요소망을 생성하는 것은 엄청난 시간과 노력이 요구되기 때문에 비현실적 일뿐더러 대부분의 경우 구현이 불가능하다. 따라서 실무에 있어 대부분의 유한요소 해석은 자동 요소망을 채택하고 있다. 하나의 요소망은 물체의 외곽에서부터 내부로 요소를 채워나가는 방식으로 생성된다.
그리고 최근 요소망 생성기법의 발달로 형상종횡비나 찌그러짐으로 문제가 되는 경우는 거의 없을뿐더러, 해석자가 임의로 요소망 밀도(mesh density, 혹은 요소 크기)를 조절할 수도 있고 또한 국부적으로 요소망을 조밀하게 생성할 수도 있다.
하지만 해석자가 간과해서는 안될 유의사항은 해석결과의 신뢰성은 요소망의 품질과 직결된다는 점과 해석하고자 하는 문제에 대해 어떠한 요소망이 최적인지를 판별할 수 있는 능력을 갖추고 있어야 한다는 점이다.
.
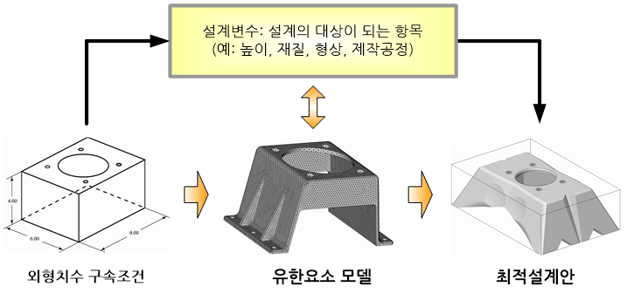
변수라는 용어는 일정한 값으로 고정되어 있지 않고 변할 수 있는 인자(factor)를 지칭한다. 예를 들어 고층 건물을 설계할 경우, 이 건물의 층수가 아직 결정되지 않은 단계라면 건물의 층수는 변수가 될 것이다. 하지만 이미 완공되어 있는 어떤 건물의 층수는 변수에 해당되지 않는다. 한편, 어떠한 현상이나 물체의 거동 혹은 성능은 수 많은 인자(factor)들의 영향을 받는다. 이러한 인자들 중에서는 변할 수 있는 것들과 일정한 값으로 고정되어야만 하는 것들로 나눌 수 있다.
어떠한 제품을 설계할 경우, 전자에 해당되는 인자들을 변수라고 부르고 후자에 해당되는 인자들을 제약 조건이라고 부른다. 변수들 중에서도 특별히 제품의 성능에 지대한 영향을 미치는 변수들을 설계변수라고 부르고, 제품 설계는 이러한 설계변수들을 결정하는 작업이라고 볼 수 있다. 참고로 동일한 제품을 설계하는 경우에 있어서도 목표로 하는 성능이 달라지면 설계변수도 달라지게 마련이다.
예를 들어, 전자제품을 설계할 경우 제품의 가격을 낮추는 것이 목표라면 구성 부품의 재료비, 제조 경비, 영업 경비 등이 주요한 설계변수가 될 것이다. 하지만 제품의 가격보다는 제품의 품질이 목표라면 구성 부품의 품질, 설계 및 제조 기술 등이 주요한 설계변수가 될 것이다. 주어진 조건 하에서 제품이 발휘할 수 있는 최고의 성능을 목표로 최적의 설계변수들의 조합을 결정하는 것을 특별히 최적설계(optimum design)라고 부른다.
.
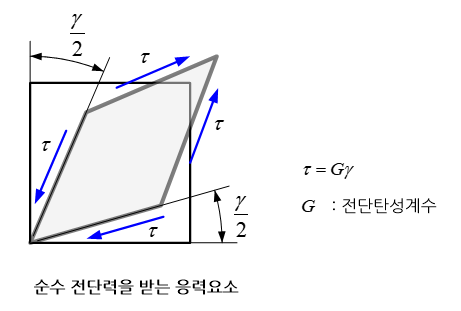
직사각형 모양을 가진 지우개의 한 면을 책상 위에 대고 지우개의 반대면을 수평방향으로 손가락으로 밀면 지우개는 더 이상 직사각형 모양을 유지하지 않는다. 다시 말해 직사각형에서 평행사변형 모양으로 변형된다. 손가락으로 밀기 전에는 지우개의 각 모서리는 직각(90도)이였지만, 변형이 된 이후 두 모서리는 90도 보다 작아지고 나머지 두 모서리는 90도 보다 커진다.
위에서 예를 든 지우개의 두 면이 이루고 있는 각도의 변화를 라디언(radian, 180도=3.14radian에 해당)으로 계산한 값을 전단 변형률(shear strain)이라고 부른다. 위의 지우개의 경우, 90보다 증가한 두 모서리와 90보다 감소한 두 모서리에서 90도로부터 증가하거나 감소한 각도의 크기는 같기 때문에 전단 변형률의 크기는 같고 기호만 서로 반대가 된다. 각도가 증가한 경우를 (+)로 그리고 각도가 감소한 경우를 (–)로 정의한다.
한편, 손가락으로 지우개 면을 수평으로 미는 총 힘을 손가락과 접촉하는 지우개의 면적으로 나눈 값을 전단응력(shear stress)이라고 부른다. 손가락으로 미는 힘이 증가할수록 지우개 모서리각의 변화도 비례적으로 증가할 것이다. 이처럼 전단변형률과 전단응력과의 상관관계를 나타내는 재료의 물성치를 전단 탄성계수라고 부른다. 다시 말해 전단응력의 크기는 전단 변형률의 크기에 전단 탄성계수를 곱한 값과 같다.
참고로 영률(Young’s modulus)이라고 불리는 탄성계수(elastic modulus)는 물체의 길이방향으로의 수직 변형률(normal strain)과 수직응력(normal stress)과의 상관관계를 나타내는 재료 물성치(material property)이다. 그리고 전단탄성계수와 탄성계수는 서로 독립적인 물성치가 아니라 프와송 비(Poisson’s ratio)를 통하여 서로 종속적인 관계를 지닌다.
.
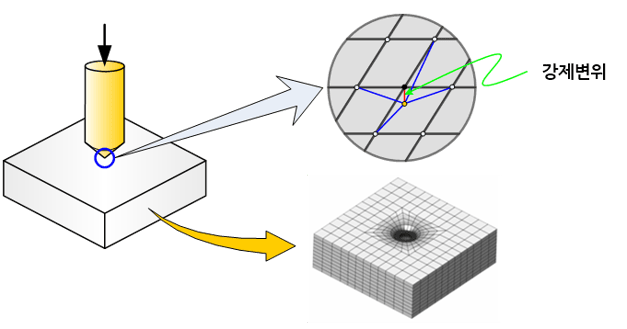
강제 변위는 용어 그 자체로는 물체에 억지로 변위를 부여한다는 의미이지만, 유한요소 해석에서는 복잡한 체결구를 대체하기 위한 수단으로 효과적으로 사용된다. 예를 들어 두 물체를 볼트를 이용하여 체결하는 과정을 수치해석(numerical analysis)적으로 구현하는 경우를 생각해 보자. 볼트 나사산과 물체 사이의 복잡한 체결상태를 재현하는 것은 상당히 어려운 작업일뿐더러, 나사산과 물체 사이의 상호적인 거동을 필요로 하는 경우는 거의 드물다. 따라서 볼트 머리와 너트 부분과 직접 접하는 물체 영역이 나사산의 회전에 따라 이동하는 과정을 강제 변위로 대체하면 손쉽게 체결과정을 구현할 수 있다.
이 외에도 강제 변위는 유한요소 해석에서 다양한 용도로 사용되고 있다. 예를 들어, 금속판을 성형하는 경우 펀치(punch)가 금속판을 누르는 과정을 강제 변위로 대체할 수 있다. 펀치와 직접 접촉하는 금속판 표면에 위치하는 절점(node)에 펀치의 이동량에 상당하는 변위를 강제적으로 부여함으로써 간략화 된 해석을 수행할 수 있다. 강제 변위는 강성이 무한대이고 질량을 가지지 않는 강체요소(rigid element), 갭요소(gap element), 슬라이드 라인요소(slide line element) 등과 개념적으로 유사하다.
.
