유한요소법(Finite Elment Method)은 물체의 영역을 유한(Finite)개의 요소(Element)라 불리는 작은 영역들로 분할하여 현상의 답을 근사적으로 구하는 수치해석 기법(Method)입니다.
목차
1. 유한요소법의 발전 과정
2. 유한요소법의 기본 개념
3. 요소(Element), 절점(Node)의 이해
4. 유한 요소 기본 이론
5. 요소 강성 행렬 구성
6. 시스템 강성 행렬 구성
7. 유한요소해석법 예제
8. 유한요소법의 대수방정식(Algebraic Equation)의 이해
1. 유한요소법의 발전 과정
유한요소법은 1930년대에 개발된 Matrix 이론을 사용하여 1950년대부터 1960년대에 걸쳐 활발히 연구가 시작되었고, 1960년대의 진공관 계산기로 구조 해석이 주로 선형 문제에 적용되었습니다. 1970년도에 상업용 프로그램들이 출시되기 시작하고 유한요소법의 적용 범위가 비선형 영역까지 확장되기 시작했습니다.
유한요소법은 방대한 계산이 필요한 관계로 컴퓨터 하드웨어의 발전과 더불어 급속히 발전하여 초기의 국방/항공/우주와 같은 대규모 국책 프로젝트에 주로 적용하였던 상황에서 자동차, 기계, 항공, 조선 분야에서도 필수적으로 활용하게 되었고, 오늘날에는 일상 생활에 필요한 단순 부품으로까지 전반적인 산업계에 확장 적용되어 유체 및 생체 공학에까지 그 응용 범위가 넓혀져 사용되고 있습니다.
1. 제 1 세대 (1950년대)
- 최초의 상용 컴퓨터
- 고가(高價)의 컴퓨터로 군사 산업 분야에 한정
- 방대한 구조 계산이 필요한 항공기 개발 분야
- 릴레이, 진공관 식
2. 제 2 세대(1960년대)
- 트랜지스터 기술 컴퓨터의 소형화 (IC)
- 다양한 유한 요소의 개발
- 유한요소법의 실용성에 대한 확인
- NASA에서 범용 프로그램 Nastran 개발 착수 (제 3 세대)
3. 제 3.5 세대(1970년대)
- 구조 공학 이외 분야 적용
- 상용 유한 요소 해석 프로그램의 등장
- 슈퍼컴퓨터 Clay-1 발표
- CAD와 연계로 산업계에 급속히 보급
4. 제 4 세대(1980년대)
- 비선형(非線型) 해석 시작
- 충격, 유체, 전자장, 음향 등 적용범위 확대
- 컴퓨터의 비약적인 성능 개선 및 Down-sizing
- Concurrent Engineering
5. 제 5 세대(1990년대)
- No production without CAE Simulation
2. 유한요소법의 기본 개념
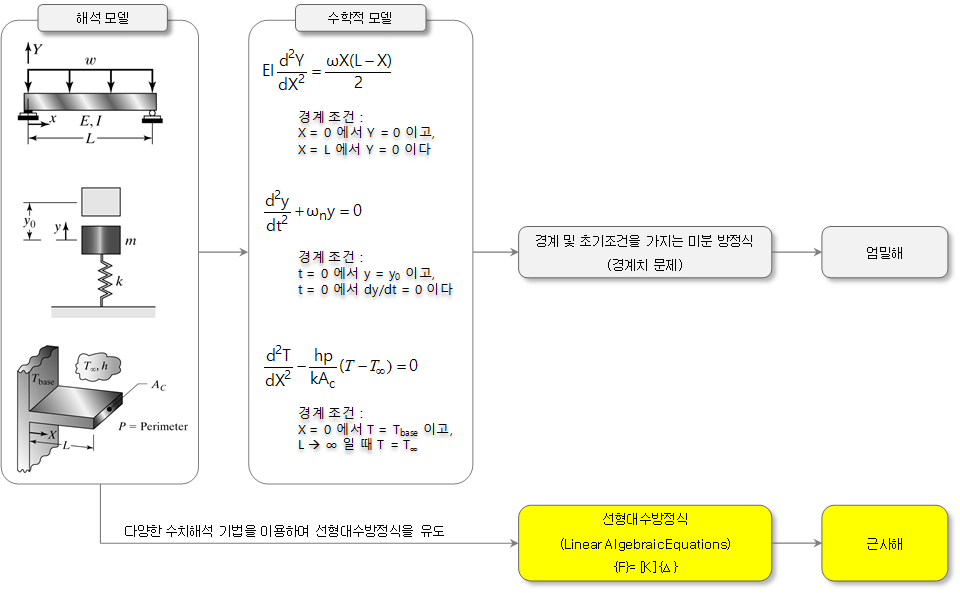
유한요소법은 공학과 수리 물리학의 문제들을 풀기 위한 수치해석 기법의 하나입니다. 일반적으로 미분방정식 형태로 구성되는 자연 현상을 선형대수 방정식 (Linear Algebraic Equation)으로 구성하여 근사해를 구하는 기법입니다.
유한요소법은 이론해를 직접 구하기 어려운 복잡한 모델을 우리가 조작할 수 있는 유한개의 요소(element)로 분할하고, 개별 요소의 특성을 계산한 다음, 전체 요소의 특성을 모두 조합하여 전체 모델의 특성을 근사적으로 계산하는 방법으로 이해할 수 있습니다.
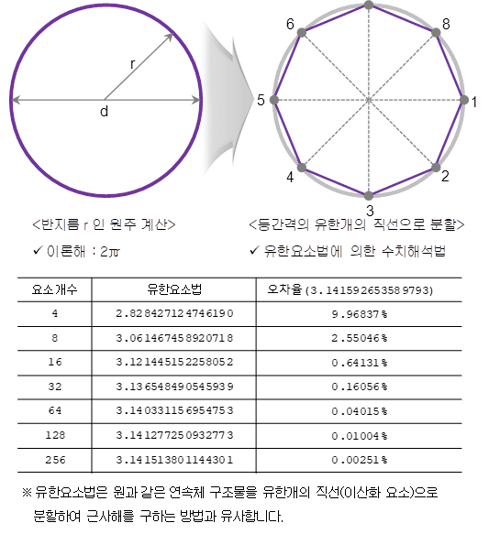
유한요소의 기본 개념은 오른쪽 그림과 같이 원주를 계산하는 것과 유사한 방법입니다. 우리는 현재 원주를 계산하는 이론해 (2πr) 를 알고 있습니다. 이 이론해를 모를 때 우측의 그림과 같이 같은 간격의 유한개의 직선으로 분할하고, 직선의 길이를 측정하면 근사하게 원주를 구할 수 있습니다. 그림의 표에 나타낸 것과 같이 직선의 수를 증가시키면 시킬수록 이론해와 유사한 결과를 얻을 수 있습니다. 즉, 유한요소법은 원과 같은 연속체 구조물을 유한개의 직선(이산화 요소)으로 나누어 근사해를 구하는 방법과 유사합니다.
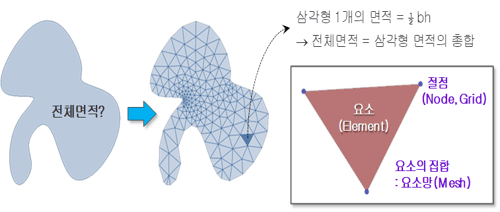
이와 유사한 개념으로 아래 그림과 같이 면적을 구하는 문제도 유한요소법의 개념과 유사합니다. 아래 그림과 같은 임의 모양의 영역의 면적을 구하는 문제에는 이론해가 존재하지 않습니다. 하지만, 만약 이 영역을 오른쪽과 같이 여러 개의 삼각형으로 나누면 삼각형 하나의 면적은 간단하게 계산할 수 있고, 영역의 전체면적은 삼각형 면적의 총합으로 근사적으로 구할 수 있습니다.
3. 요소(Element), 절점(Node)의 이해
요소는 유한요소법에 있어 가장 기본이 되는 사항입니다. 요소의 역할은 유한개의 요소를 이용하여 해석하고자 하는 대상물의 형상을 구성하는 데 있습니다. 요소를 이용하여 생성한 모델을 유한요소 모델 또는 수치해석 모델, 이산화 모델(Discrete model), 이상화 모델(Idealization model)이라고 정의합니다. 유한개의 요소를 이용하여 정의되는 해석 구조물의 형상은 재료 물성값과 요소 특성치가 더하여 해석하고자 하는 대상 구조물의 주요 특성인 강성을 정의하는 데 사용됩니다.
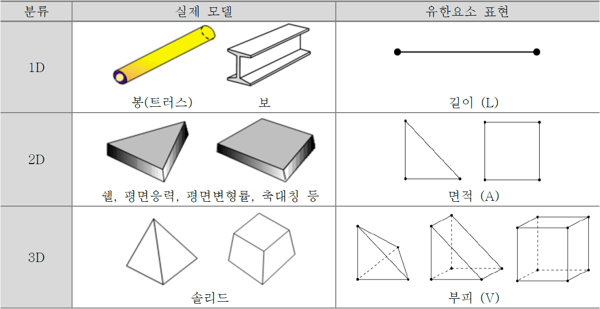
유한요소의 종류는 크게 1차원, 2차원, 그리고 3차원 요소로 나눌 수 있습니다. 각 차원의 요소를 명확하게 이해하기 위해서는 요소 특성치와 같이 이해하는 것이 좋습니다. 요소의 차원과 요소 물성값의 기본 개념은 어떻게 3차원 형상으로 표현을 가능하게 하는가가 주요 사항입니다.
요소의 차원 및 기하학적 형상에 의한 분류는 1차원 요소(선), 2차원 요소(삼각형/사각형), 3차원 요소(사면체/오면체/육면체/피라미드)로 구분할 수 있으며, 주요 형상은 다음 그림과 같습니다. > 요소와 절점 더 자세히 보기🔎
요소의 종류와 활용 방법에 대해
더 자세히 알아보기(클릭)👇
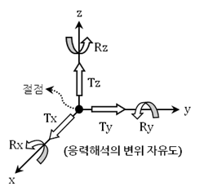
유한요소법에서 결과(미지수)가 계산되는 위치를 절점(Node)이라 하고, 일반적으로 요소의 꼭짓점입니다. 절점은 요소의 모양과 위치를 정의하고, 또 결과가 계산되는 중요한 위치입니다. 그리고 절점의 미지수를 자유도(degree of freedom, DOF)라고 합니다.
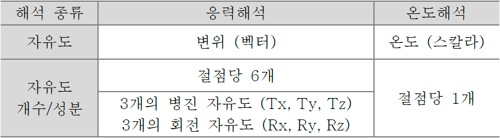
절점의 미지수는 해석 종류와 요소 종류에 따라 자유도의 물리적 의미와 절점이 갖는 자유도의 종류와 개수가 달라집니다. 기본적인 응력 해석을 수행할 때에는 절점이 원래 위치에서 얼마큼의 변형이 발생했는가가 주요한 미지수입니다. 응력 해석의 경우 절점이 얼마만큼 이동하였는지는 6개의 변위 자유도 성분으로 표현합니다.
4. 유한 요소 기본 이론
일반적으로 유한요소법은 크게 다음과 같은 절차를 통하여 계산됩니다.
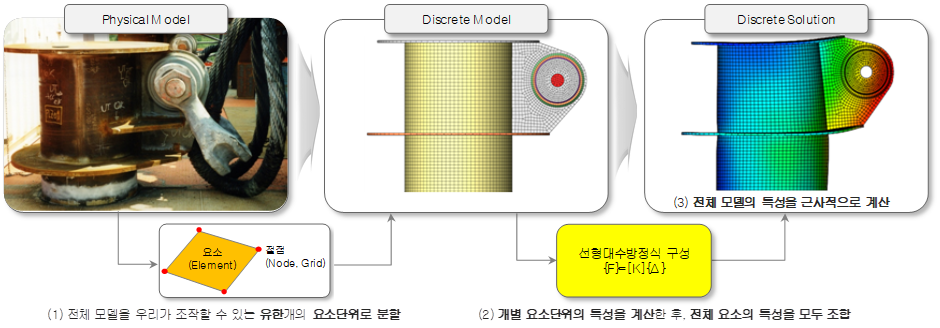
<유한요소법의 해석 절차>
1. 전체 모델을 우리가 조작할 수 있는 유한개의 요소 단위로 분할
2. 개별 요소 단위의 특성을 계산 (요소 강성행렬)
3. 전체 요소의 특성을 모두 조합 (시스템 강성행렬)
4. 전체 모델의 특성을 근사적으로 계산
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.






.png?width=700&name=%EC%A0%9C%EB%AA%A9%EC%9D%84%20%EC%9E%85%EB%A0%A5%ED%95%B4%EC%A3%BC%EC%84%B8%EC%9A%94_-012%20(2).png)










