최적 설계는 설계에 주어진 모든 제약 조건을 만족하면서 가격이 가장 낮은 설계를 의미한다. 따라서 이런 최적 설계 문제를 정식화하면 다음과 같이 수학적 문제로 변환할 수 있다.
목차
1. 서론
2. 경사도 기반 해법(Gradient based method)
3. 민감도 미사용 해법(Non-gradient based method)
4. 엑셀을 이용한 해법
1. 서론
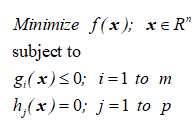
m개의 부등호 제약 조건 g(x)와 p개의 등호 제약 조건 h(x)를 만족하면서 목적 함수 f(x)를 최소화하는 n개의 실수인 설계 변수 x를 구하는 문제가 된다. 이런 최적화 문제는 카러쉬쿤터거 필요 조건(Karush-Khun-Tucker necessary condition)을 만족하는 해를 구함으로써 해석적으로 풀 수 있다.
그러나 함수의 비선형성이나 제약 조건이 많은 경우는 이 해석적 방법으로 해를 구하는 것은 매우 어렵다. 많은 공학설계문제에서는 해석적 방법이 적절하지 못하다. 따라서 이런 공학 문제의 최적화를 위한 체계적인 수치 해석 기법이 필요하다. 수치 해석 법에서는 초기 설계를 설정하고 이 설계 변수를 최적성 조건을 만족할 때까지 반복적으로 구한다.
최적화 문제의 일반 알고리즘은 다음의 반복과정으로 표현된다.
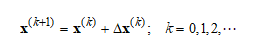
이 식에서 상첨자 (k)는 반복 수를 나타내며, Δx(k)는 (k) 번째 설계 단계에서의 설계 변수 변화량을 나타내며 벡터 성분인 탐색 방향 d(k)와 양의 스칼라인 이동 거리 α(k) 로 분리하여 다음과 같이 표현한다.
따라서 비제약 최적 설계 문제나 제약 최적 설계 문제에 모두 적용할 수 있는 일반 알고리즘은 다음과 같이 정리할 수 있다.
단계 1 : 초기 설계 변수 (x_0)를 설정하며, 반복 회수 k=0으로 한다.
단계 2 : 탐색방향 (d_k)를 계산한다.
단계 3 : 알고리즘의 수렴성을 검토하여 수렴하면 종료하고 그렇지않으면 계속한다.
단계 4 : 양의 이동거리 (α_k)를 계산한다.
단계 5 : 새로운 설계 변수를 다음과 같이 구한다 : (x_(k+1))=(x_k)+(α_k)⋅(d_k)
단계 6 : k=k+1 으로 두고 단계 2로 간다.
2. 경사도 기반 해법(gradient based method)
탐색 방향을 결정하는 데 경사도를 이용한다. 2차 미분값을 사용하면 수렴 속도는 개선되나 헤시안 행렬의 계산이 많은 시간이 요구되므로 헤시안 행렬을 근사적으로 구하는 유사 뉴튼법이 제안되었으며 DFP(Davidon, 1959; Fletcher and Powell, 1963)법과 BFGS(Broyden-Fletcher-Goldfarb-Shanno)법이 있다.
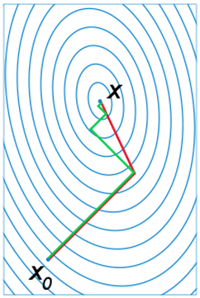공액경사법(conjugate gradient method)
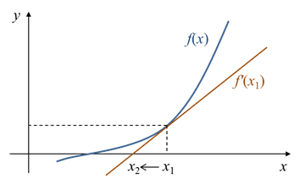뉴튼법(Newton’s method)
국부 최적해(local optimum)를 효율적으로 탐색하는 전략을 사용하는데, 이러한 방법은 이론적인 측면에 있어서는 전역 설계해(global optimum)를 보장하기 어려울 뿐 아니라 설계비용 측면에 있어서는
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
