흔히 FSI(Fluid-Structure Interaction)해석으로 통용되는 유체-구조 연계 해석은, 유체 유동과 구조물 변형 (혹은 운동)이 상호 영향을 끼치는 시스템의 동적 응답을 다루게 된다. 엄밀한 의미에서, 지구 상의 모든 물체는 기체 혹은 유체와 항상 접하고 있다. 다만, 기체나 유체의 영향력이 현저하지 않기 때문에 유체-구조 연계 문제로 간주하지 않을 뿐이다. 풍력 발전 시스템, 빗길을 주행하는 타이어 그리고 항해 중인 LNG선과 같은 구조물의 경우, 접하고 있는 공기나 유체와의 상호작용은 결코 무시할 수 없다.

그림 1: 해상 풍력발전시스템(sea wind turbine)
유체-구조 연계 해석은 유체 유동과 구조물의 동적 응답을 동시에 계산해야 하므로, 시간 적분(time integration)과 두 거동 사이의 연계(coupling) 처리가 요구된다. 이러한 두 작업은 정해석(static analysis)에 비해 요구되는 CPU 시간이 엄청나므로, 유체-구조 연계시스템의 규모와 복잡성이 증가하게 되면 슈퍼컴퓨터를 사용하더라도 해석이 쉽지 않을 수 있다.

그림 2: 빗길을 주행하는 타이어의 수막현상
이번 칼럼에서는 이러한 대규모(large-scale) 유체-구조 연계 문제를 효과적으로 처리하기 위한 연계 해석기법을 소개하고자 한다. 이 기법은 전역-국부 접근방식(global-local approach)과 적응적 FSI기법으로 이루어져 있으며, FSI해석에 있어 관심의 대상이 시스템의 모든 지점 그리고 모든 시점에 있지 않다는 사실에 기초하고 있다.

목차
1. 유체-구조 연계 문제(Fluid-structure linkage system)
2. 동역학적 기술법(Kinematic description)
3. 연계 기법(Coupling method)
4. 적응적 FSI기법(Adaptive FSI method)
1. 유체-구조 연계 문제
유체 유동을 표현하는 포텐셜 혹은 Navier-Stokes 이론과 구조물의 동적 거동을 표현하는 운동방정식을 수치적으로 연계시키는 방법은 크게 직접법(monolithic)과 시차체 반복법(staggered iterative)의 두 가지로 분류할 수 있다.
직접법은 두 개의 수학 방정식을 근사화 하여 하나의 행렬 방정식으로 통합하는 것으로, 두 거동의 연계 효과가 이 행렬 방정식에 자동으로 포함되기 때문에 추가적인 연계 처리를 필요로 하지 않는다. 하지만, 연계시스템의 규모가 커지고 복잡성이 증가하게 되면, 행렬이 거대화 되어 행렬 저장과 계산에 어려움이 따르게 된다.
반면, 시차제 반복법은 각 거동에 대한 행렬방정식들을 하나로 통합하지 않고, 두 행렬방정식을 지그재그 방식으로 풀어나가면서 상호 연계 효과를 반영한다. 이 방식은 지그재그로 풀어나가는 과정에서 매번 연계 효과를 반영해야 하는 단점이 있지만, 행렬방정식이 과도하게 대형화되는 것을 억제할 수 있다.

그림 3: Staggered iterative 연계 해석기법
상용 FEM Code에서는 후자의 방식을 채택하고 있는데, 그 이유로는 앞서 설명한 행렬의 거대화 이외에도 모듈 단위로 개발된 솔버들을 연계시키기에 편리한 장점을 제공하기 때문이다.

2. 동역학적 기술법 (Kinematic Description)
유체-구조 연계 해석 기법을 구분하는 다른 하나의 기준으로 동역학적 기술법이 있다. 구조물의 경우에는 파쇄와 같이 특별한 경우를 제외하고는, Lagrange 기술법의 FEM으로 근사화하는 것이 일반적이다. 반면, 유체유동의 경우에는 격자를 Lagrange, Euler 그리고 ALE(arbitrary Lagrangian-Eulerian) 기술법 중 어느 하나를 기준으로 생성할 수 있다.
Lagrange 기술법에서는 유체입자가 격자와 함께 이동하기 때문에 자유표면과 같은 유체 경계가 자동으로 정의된다. 하지만, 유동이 복잡한 경우에는 요소가 과도하게 찌그러져, 시간 적분 과정에서 요소망을 조정해야 하는 번거로움이 따른다.
반면, Euler 기술법에서는 격자망이 공간상에 고정되어 있으므로 격자의 찌그러짐은 발생하지 않지만, 요소 내 유체가 차지하는 상대 체적비로 유동을 표현하기 때문에, 자유표면 추적(free surface tracking)을 위한 부가적인 작업이 필요하다.
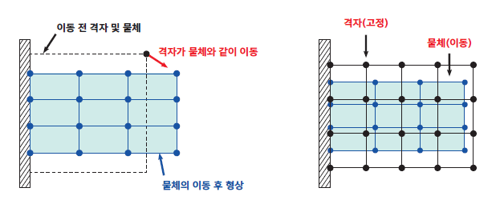
그림 4: Lagrange 및 Euler 격자망
ALE 기술법은 Lagrange와 Euler 기술법의 장점만을 채용한 것으로서, 유체의 경계에는 Lagrange 요소망을 그리고 유체 내부에는 Euler 격자를 혼용하는 기술법이다. 따라서, ALE 기술법은 요소의 찌그러짐과 자유표면 추적을 가장 효과적으로 처리할 수 있다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.

















