조금 불편해도 2D 요소를 무조건 사용해야만 하는 이유는?

사실 솔리드 요소에 비하면 판/쉘 요소는 어느 정도의 역학적 기초 지식이 필요하다. 그럼에도 불구하고 판/쉘 요소가 중요한 이유는 나날이 그 필요 또는 사용이 증대되어 가는 복합 재료에 있다. 복합 재료를 3차원 솔리드 요소로 해석해 본 경험이 있는 유저들은 알 수 있을 것으로 생각하는데, 정확한 응력분포를 계산하기 위해서는 많은 수의 요소가 필요하다.

때로는 단순한 판 형상에 대해 500만 자유도를 넘어가기도 한다. 일반적인 PC에서는 해석 불가하고, 36G 정도의 램을 가지고도 해석 시간은 짧지 않다. 특히 비선형 해석이나, 동적 해석을 할 경우 계산 시간은 기하급수적으로 증가하게 된다.

대부분의 상용 프로그램에서 복합 재료 특히 적층 복합 재료(laminated composites)에 대해서는 판/쉘 요소를 권장하는 이유이기도 하다. 판/쉘 요소를 중심으로 그 기반이 되는 변분법과 판/쉘 이론들 사이의 상관관계에 대하여 소개하고자 한다.

1. 서론

유한요소법은 지난 50년간 많은 발전이 있었다, 현재 많이 쓰이고 있는 하이브리드 응력 요소(hybrid stress element)는 1964년 Pian에 의해 개발되었다. 초기에는 주목받지 못하다가 1970년대 후반부터 급격하게 발전하였고 본격적으로 상용 프로그램에 쓰이기 시작한 것은 1990년대 후반 이후이다. 하이브리드 요소의 급격한 발전에는 변분 원리(variational principle)가 성장의 큰 축을 담당하였다. 특히 3차원 또는 2차원 하이브리드 요소의 발전은 Hellinger -Reissner의 혼합 변분 이론을 기반으로 개발된 다양한 형태의 변분 원리가 그 이론적 기저로 작용하였다. 변위 기반 요소보다 성능이 뛰어나기 때문에 현재 대부분의 상용 프로그램에서 기본 솔리드 및 평면 요소로써 사용되고 있다.

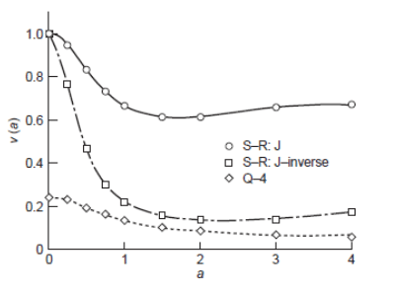
하이브리드 요소(S-R)의 성능

그림 1: 하이브리드 요소(S-R)의 성능

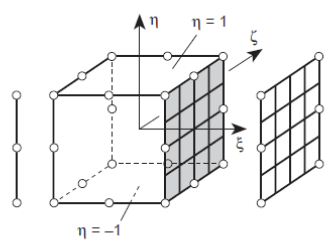
솔리드(Solid) 요소의 로컬 좌표계

그림 2: 솔리드(Solid) 요소의 로컬 좌표계

이러한 3차원 요소의 발전과는 대조적으로 판/쉘 요소는 학계에서는 (특히 학술 저널인 International Journal for Numerical Methods in Engineering을 중심으로) 많은 다양한 요소들이 개발되었지만, 상용 프로그램에서의 활용은 상대적으로 미미하다고 할 수 있다. 판/쉘 요소는 솔리드 요소에 비해 실제 응용 문제에 적용할 때 기하학적인 표현에 있어 제약이 있기 때문이다. 유저 입장에서 보면 CAD 데이터만 있으면, 자동으로 해석을 해주는 프로그램이 사용하기 편한 것은 주지의 사실이다.

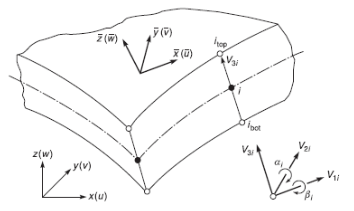
쉘(Shell)의 요소의 좌표계

그림 3: 쉘(Shell)의 요소의 좌표계

2. 고전적 판/쉘 이론

상용 유한요소 프로그램에서 주로 발달한 요소는 고전적 이론에 기초한 판/쉘 요소보다는 일차 전단 변형 이론에 기초한 요소가 수치 및 해석의 용이성 때문에 주로 쓰인다. 그럼에도 불구하고 이 절에서는 판/쉘 요소가 어떻게 해서 만들어지는지에 대한 소개의 관점에서 고전적 이론을 다루기로 한다.

얇은 판/쉘 이론은 다음과 같은 단순한 형태의 변위장으로부터 출발한다.

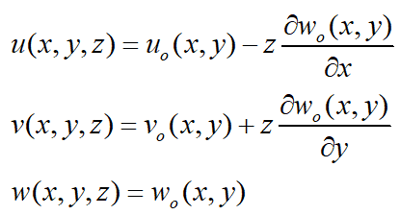
단순한 형태의 변위장 계산식

위의 식에서 보여지듯 변위장은 횡 방향 전단 변형률과 수직 변형률은 고려하지 않는다. 이러한 판/쉘 이론의 (수치적 관점에서) 장점으로는 두께 방향 (즉, z축 방향)으로의 적분을 해석적으로 수행함으로써 컴퓨터의 계산 시간을 줄일 수 있다는 것과 판/쉘 구조물이 매우 얇은 경우에도 수치적인 문제가 발생하지 않는다는 것이다. 하지만 고전적 이론의 단점도 존재하는데, 상대적으로 두꺼운 구조물은 기본 가정상 계산할 수 없다는 것과 에너지에 처짐의 두 번 미분한 것이 들어오기 때문에 형상 함수가 C1 연속 조건을 만족해야 한다는 것이다. 특히 후자의 이유로 현재 상용 프로그램들은 일차 전단 변형 이론(Reissner-Mindlin, 1945, 1951)에 기초한 요소들을 보다 더 많이 가지고 있다.

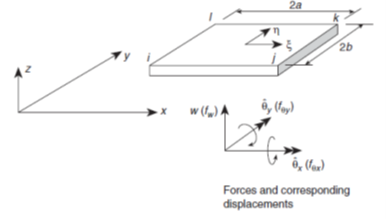
직각 판 요소의 좌표계 및 회전 벡터