문제 풀이로 본 유한요소법과 유한차분법의 차이점
1. 서론
제품 개발에 있어서 유한요소법(FEM)이 신뢰성 검증에 매우 광범위하게 적용되고 있다는 것은 주지의 사실이다. 유한요소법 이론은 이미 상용화된 유한요소해석 코드 (또는 소프트웨어)로 널리 보급되었다. 또한 상용 코드의 사용자 편의성이 향상됨에 따라 제품 설계자 또는 해석 엔지니어가 쉽게 활용할 수 있는 방법이 되었다.
한편 유한차분법(FDM)도 제품 개발에 있어서 특정한 분야 (예, 유동 해석 등)에 활용되고 있다. 유한요소법과 유한차분법은 용어에 있어서 비슷하지만, 그 의미와 적용 방법은 매우 다르다고 할 수 있다. 두 방법 모두 궁극적으로는 대수 방정식(행렬)을 이용하여 원하는 해를 구하는 점에서는 동일하지만, 정식화 과정과 특징이 매우 다르다.
본 기사는 상미분 방정식(Ordinary Differential Equation)을 대상으로 FDM과 FEM을 적용하여 해를 구하는 과정을 사례로 설명하고, 두 방법의 특징을 간략하게 비교하였다.
통상적으로 엔지니어가 접하는 상당수 문제는 미분 방정식으로 표현된다. 특히 힘과 모멘트 평형, 관성의 법칙, 작용과 반작용의 법칙, 운동량 보존의 법칙, 에너지 보존 법칙 등과 같이 고전적인 뉴턴 역학 법칙을 바탕으로 정립된 동역학, 구조 역학, 유체 역학의 현상은 대부분 편미분 방정식 또는 상미분 방정식으로 표현된다.
엔지니어는 이러한 미분 방정식의 해를 구함으로써 분석하고자 하는 시스템의 거동을 예측하고 평가하는 것이 가능하다. 미분 방정식의 해를 구하는 방법으로는 해석적인 방법, FEM, FDM, 그리고 경계 요소법과 같은 방법 등 다양한 수학적 기법이 적용된다.
본 기사는 식(1)에 제시한 상미분 방정식을 대상으로 FDM, FEM을 적용하여 그 해를 구하는 과정을 통해서 간접적으로 FDM과 FEM의 특징을 설명하고자 한다.
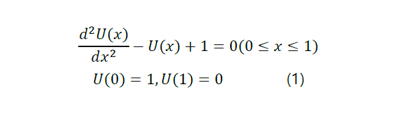
먼저, 식(1)을 해석적인 방법을 적용하여 해를 구하면 아래와 같다.
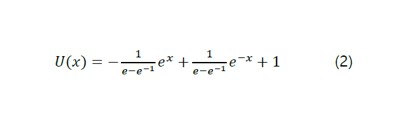
2. 유한차분법을 이용한 해석
유한차분법은 일반적으로 수치 해석이라는 용어로 소개되거나 설명되고 있다. 아래의 그림은 해 영역을 몇 개의 점으로 분할한 것을 보이고 있다.
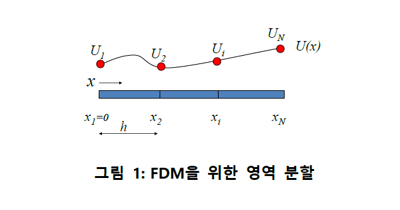
유한차분법은 미소 증분을 이용하여 미분 항을 대수 방정식으로 변환하여 해를 구하는 방법이다. 식(1)에 보인 항목 중에 2계 미분항을 미소 증분으로 표현하면 아래와 같다.
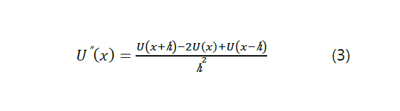
(중략)
3. 유한요소법을 이용한 해석
FDM과 마찬가지로 FEM 도 미분 방정식을 푸는 방법의 하나이다. 최종적으로 FEM도 미분 방정식을 대수 방정식으로 변환하는 점에서는 FDM과 유사하다고 할 수 있다. FDM은 미분 항을 미소 증분으로 표현하는 특징이 있으나, FEM은 에너지 방법, Weak form 방법 등을 거쳐서 지배 방정식 자체를 대수 방정식으로 표현하는 과정이 필요하다. 또한 보간 함수(Shape function)을 적용하는 과정이 필요하다. 그 과정은 아래와 같다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.

















