응력이 집중되는 지점에서 구조물의 파손이 시작되기 때문에 응력집중의 크기를 정확하게 예측하는 것은 구조해석의 궁극적인 목표입니다. 하지만, 유한요소 해석에 있어 응력이 집중되는 지점에서 물체의 거동을 정확하게 예측하는 일은 실로 대단히 어려운 일입니다. 가장 대표적인 예로 균열(crack) 선단에서의 응력집중 형상을 들 수 있으며, 신경을 쓰지 않고 해석을 수행하게 되면 엄청나게 낮은 응력값만 구하게 됩니다.
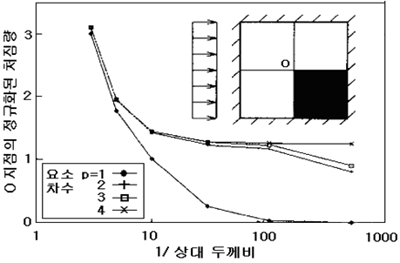
그림 1. 요소망의 영향 : 중앙부 처짐량의 큰 오차
한편, 두꺼운 판재에 비해 박판 구조물이 유한요소 해석이 쉽다고 생각하기 쉬우나, 정반대로 박판 구조물은 유한요소 해석이 난해하기 그지없습니다. 그 이유는 길이에 비해 구조물의 상대 두께가 감소하게 되면 잠김 현상과 경계층 효과라는 특이한 현상이 발생하기 때문입니다.
그림 1과 2는 수직분포 하중을 받는 박판의 중앙지점에서의 변형과 폭 방향으로의 전단력 분포를 나타내고 있습니다. 그림 1은 두께 비가 줄어들면 저차 요소에서 변형량이 0으로 줄어드는 것을, 그리고 그림 2는 엉성한 균일 요소망은 오차가 큰 횡 전단력을 나타냅니다.
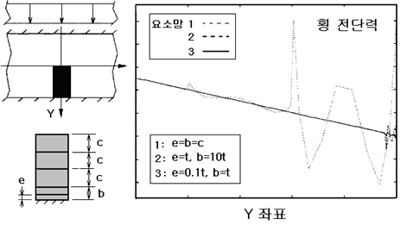
그림 2. 요소망의 영향 : 전단 응력에서의 큰 오차
응력집중, 잠김 현상 그리고 경계층 효과는 해석을 위해 생성한 요소망에 크게 좌우됩니다. 한편, 이러한 현상들은 비단 구조해석에만 한정되지 않고, 대부분의 해석 문제에서 함께 발생합니다. 따라서, 이러한 현상들을 정확하게 재현하거나 방지할 수 있는 효과적인 요소망 생성은, 해석자라면 누구나 숙지해야 할 필수적인 해석 기술입니다.
본 칼럼에서는 이러한 현상들의 특성을 보다 상세히 살펴보고, 이러한 현상들을 효과적으로 재현하거나 방지할 수 있는 요소망을 생성하는 방법을 설명하고자 합니다.

목차
1. 응력 집중(Stress concentration)
2. 잠김 현상(Locking phenomenon)
3. 경계층 효과(Boundary layer effect)
4. 효과적인 요소망 생성 방법(How to generate mesh effectively)

1. 응력 집중
대상이 되는 물체의 기하학적 영역 내에서 형상이 180º 이상 꺾이는 지점에서는 반드시 거동의 집중 현상이 발생합니다. 다음의 그림 3에서 좌측의 L자 형상의 코너부의 꺾임 각은 270º로써 현저한 응력 집중 현상을 나타냅니다. 이러한 특징 형상 외에 하중 및 구속 조건이 매우 좁은 면적에 집중될 때 그리고 항공기 날개 주위 유동장의 충격파(shock wave) 전후의 예리한 불연속이 응력 집중 현상을 유발합니다.
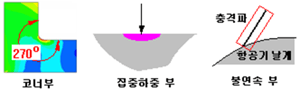
그림 3. 응력 집중을 야기하는 특징 형상, 집중 하중/구속 및 불연속 부위
이렇게 꺾임 각이 180º 이상이 되는 지점에서 거동이 급격하게 큰 값으로 급등하는 현상, 일명 해의 특이성(singularity)은 이론적으로 규명할 수 있습니다. 이론적 분석에 따른 주요한 두 가지 사항은 첫째 꺾임 각이 증가할수록 해의 특이성이 증가하며, 둘째로 상태 변수의 급증은 거의 미미하지만 상태 변수의 미분값이 급등한다는 사실입니다.
아래 그림 4에 도시한 균열 선단부는 꺾임 각이 360º로써 균열 선단으로 갈수록 응력은 가장 심한 응력 집중을 나타내지만, 변위의 증가는 거의 미미한 수준입니다. 유체 유동의 경우를 예를 들면, 꺾어진 부분에서 유속의 변화는 심하지 않지만, 유동 압력은 급격히 증가하게 됩니다.
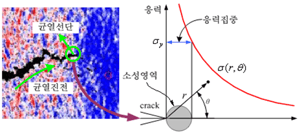
그림 4. 균열 선단에서의 응력 집중 현상
결국, 어떠한 유형의 해석에 있어서 대상이 되는 물체의 기하학적 형상에서 180º 이상으로 꺾이거나, 하중 혹은 변위 구속이 매우 좁은 면적에 가해지는 경우 그리고 불연속 계면에서는 반드시 집중 현상이 발생한다는 사실을 명심해야 합니다.

2. 잠김 현상
유한요소해석은 자연 현상에 대한 수학적 표현식을 행렬 방정식으로 전환하여 근사해를 구하는 수치 기법입니다. 그리고 행렬 방정식은 한정된 차수의 급수 함수를 이용하여 유도되기 때문에 항상 오차(error)를 수반합니다. 이러한 오차를 수치해석 오차라고 부르는데, 이 오차에 영향을 미치는 주요한 인자는 요소의 크기(h)와 요소의 차수(p)입니다.
수치해석 오차의 가장 대표적인 특징은 요소 크기가 줄어들거나 요소 차수가 증가함에 따라 감소한다는 것입니다. 그리고 이러한 오차 감소의 정도를 log 스케일로 측정하게 되면 일정한 기울기를 지닌 직선이 되는데, 이 직선의 기울기를 수렴률(convergence rate)이라고 합니다.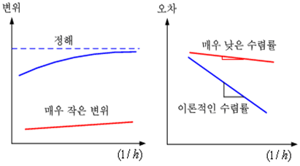
그림 5. 박판 구조물 해석의 잠김 현상
(a) 0에 가까운 변위값 / (b) 비정상적으로 낮음 수렴률
수학적인 연구에 따르면 균일한 요소 차수와 요소 크기를 지닌 요소망은 요소 크기를 줄이게 되면 요소 차수에 상응하는 수렴률을 나타낸다. 하지만 잠김 현상이 발생하면 요소 크기를 줄이더라도 매우 낮은 변위값과 이론적인 수렴률보다 현저히 낮은 수렴률을 나타냅니다.
잠김 현상은 대상이 되는 해석 문제에 어떠한 형태일지라도 반드시 만족해야 할 조건(constraint)이 수반될 때, 요소 차수가 낮은 엉성한 요소망으로 유한요소해석을 수행하면 발생하는 현상입니다. 대표적인 조건으로는 구조물의 두께가 감소함에 따라 횡 전단력이 0으로 접근해야 하는 조건(일명, Kirchhoff 조건)과 비압축성 물체나 유동에 있어 부피 변화가 없어야 한다는 조건 등을 들 수 있습니다.
예를 들어, a=b라는 조건식이 수반하는 문제를 요소 차수가 낮은 엉성한 요소망으로 해석을 수행하게 되면, 이 조건식이 a=b가 아니라 a->0, b->0라는 전혀 엉뚱한 방식으로 만족하게 됩니다. 그 결과, 근사해와 직간접적으로 연관된 a와 b가 0으로 근접하게 되어 결국 0에 가까운 근사해에 도달하게 되는 것입니다.


😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.

















