스프링 상수가 K인 선형(linear) 코일스프링에 F라는 힘으로 잡아 당길 경우 늘어나는 길이가 d라고 하면, 2F의 힘을 가하게 되면 늘어나는 길이는 2d가 될 것이다. 그리고 반대로 F/2의 힘을 가하게 되면 늘어나는 길이는 그 절반이 될 것이다. 이 문제의 특징은 스프링에 가해지는 하중의 크기만 다를 뿐, 스프링의 크기 및 강성 그리고 늘어난 길이를 계산하는 방법에는 아무런 변화가 없다는 점이다.
이렇게 단순한 1 자유도(degree of freedom) 문제를 무한개의 스프링들이 밀집되어 있다고 생각할 수 있는 탄성체(continuum body)로 확장시켜 보자. 그리고 스프링에 가해졌던 하중이 달라졌던 것과 같이 이 탄성체에 가해지는 하중조건이 달라짐에 따라 변형이 어떻게 변할 것인지를 분석하는 문제를 생각해 보자. 이 문제에 대한 유한요소 근사화는 [K]{u}={F}라는 행렬 방정식을 푸는 문제로 귀착된다. 여기서 [K]는 물체의 기하학적 형상, 재료 물성치(material property), 요소망(mesh) 그리고 변위 경계조건(displacement boundary condition)에 의하여 결정되는 강성행렬(stiffness)이다. 그리고 {F}와 {u}는 각각 가해진 하중에 대한 하중벡터(load vector) 그리고 구하고자 하는 탄성체의 변위를 나타낸다.
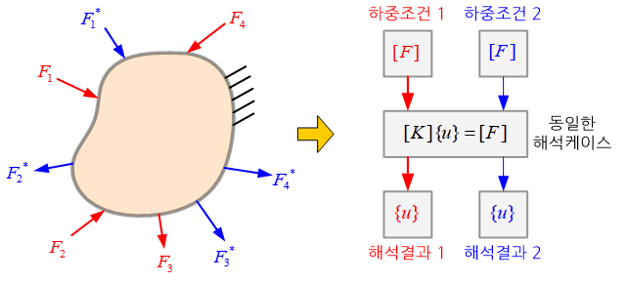
앞서 코일 스프링의 늘어난 길이를 계산하는 것과 동일하게 이 경우에도 하중벡터만 달라지는 특징을 지니고 있다. 따라서, 하중벡터만 변화시키면서 탄성체의 변형을 구할 수 있는데, 이러한 수치기법을 다중 해석이라고 부른다. 그리고 각각의 하중벡터는 서로 다른 하중조건을 각기 하나의 하중 케이스로 정의하여 설정한 다중 하중 케이스(multi-load case)로부터 손쉽게 계산할 수 있다.
다중 해석은 하나의 해석문제를 계산하는 경우와 비교하여 그 방법과 절차가 동일하기 때문에 한 번의 전처리(preprocessing) 작업만으로 여러 하중조건을 다룰 수 있기 때문에, 해석을 위한 노력과 해석시간을 대폭적으로 줄일 수 있는 장점을 지니고 있다. 그리고 현재 시판되고 있는 대부분의 상용 유한요소해석 프로그램은 이 기능을 제공하고 있다.
.