이번 포스팅에서는 무차원수가 무엇이고 왜 쓰는지, 열 및 유동 해석에서 자주 사용되는 대표적인 무차원수의 종류와 의미를 알아보겠습니다. 무차원수의 대략적 의미를 기억한다면 추후 CFD 기초 이론 학습 과정에서 이해가 훨씬 쉬워지고 학습 진행에 큰 도움이 될 것입니다.
이전 포스팅인 ‘CFD가 처음이라면 알아야 할 것들’에서 말씀드렸던 것처럼, 유체 역학과 열역학은 기계 분야에서 아주 밀접한 관련이 있으며 서로 많은 부분을 공유하기도 합니다. 마찬가지로 무차원수 또한 열과 유동이 밀접한 관계에 있는 경우가 많기에 열에 대한 무차원수와 유동에 대한 무차원수를 구분하지 않고 포괄적으로 설명 드립니다.
이전 포스팅 보러가기 👇(클릭)
목차
1. 무차원수 (Dimensionless numbers)
2. 레이놀즈수 (Reynolds number; Re)
3. 레일리수 (Rayleigh number; Ra)
4. 그라쇼프수 (Grashof number; Gr)
5. 프란틀수 (Prundtl number; Pr)
6. 너셀수 (Nusselt Number; Nu)
7. CFL수 (Courant-Friedrichs-Lewy number; CFL number; Courant number)
8. 종합 정리
1. 무차원수(Dimensionless numbers)
무차원수는 이름 그대로 차원이 없는 수입니다. 다만 차원의 의미가 직관적으로 떠오르는 내용과 다를 수 있습니다. 공간적인 개념으로는, 점이 모여 선이 되고(1차원), 선이 모여 면이 되고(2차원), 면이 모여 공간(3차원)을 이루게 됩니다.
여기에 시간 개념이 추가된다면 4차원을 떠올릴 수도 있고, 공간과 관계없이 특정 점에서 단순 화학식 계산을 하는 경우에는 0차원 해석이라고 표현하기도 합니다. 하지만 이번 포스팅에서 말씀드리는 무차원의 의미는 공간적 개념보다는 ‘단위’의 의미로 생각하시면 되겠습니다.
유체 역학에서는 dimension에 대해 설명할 때 [M], [L], [T], [Θ]로 표현합니다. [M]은 질량을, [L]은 길이를, [T]는 시간을, [Θ]는 온도를 의미합니다.
SI 단위계인지 BG 단위계(ft, slug 등을 사용)인지 관계없이, 위 정의를 바탕으로 차원 형태로 물리량을 표현할 수 있습니다. 예를 들어 속도는 MT^-1, 가속도는 MT^-2, 뉴턴 2법칙 F=ma에서 F는 MLT^-2로 표현할 수 있습니다.
무차원수는 여러 변수를 곱하고, 더하고, 나누는 등의 조합을 통해서 위에서 설명한 M, L, T, Θ의 단위를 모두 없앤 수입니다. 예를 들어 Mach number는 유체의 속도를 음속으로 나눈 수입니다. 속도를 속도로 나누었기 때문에 Mach number는 단위가 없는 수가 되죠.
이렇게 하면 음속 대비 유체의 속도가 어느 정도인지를 한 번에 파악하기 편해지며, 속도가 아닌 다른 물리량과의 연산이 가능해집니다. 다시 말해서, 단위가 없이 상수만 남도록 무차원수를 만드는 이유는 서로 단위가 다른 물리량 간에 비교나 연산이 가능하도록 하면 공학적인 문제 풀이 과정이나 물리 현상을 연구하는데 있어서 매우 편리해지기 때문입니다.
2. 레이놀즈수(Reynolds number; Re)
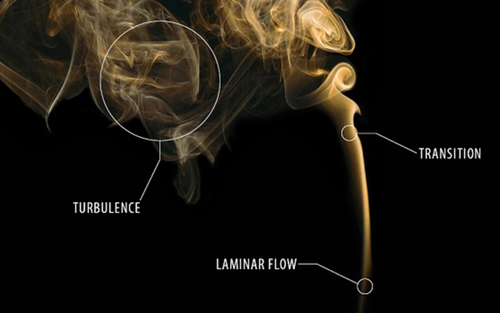
레이놀즈수를 알면 대략적인 유동 상황을 가늠할 수 있습니다. 일반적으로 레이놀즈수가 작으면 잔잔하고 가지런한 유동(층류) 상태를 떠올릴 수 있고, 레이놀즈수가 크면 복잡하고 구불구불한 유동 상태(난류)를 떠올릴 수 있습니다. 경우에 따라서는 구불구불한 와류가 없더라도 대형 선박 주위의 유동처럼 아주 큰 스케일에 대한 유동인 경우에도 레이놀즈수가 크며, 와류가 없더라도 속도가 매우 빠른 경우에도 레이놀즈수는 커집니다.
어떻게 위와 같이 예측이 가능한지는 물리적인 정의를 살펴보면 쉽게 이해할 수 있습니다. 레이놀즈수의 정의는 아래 수식과 같습니다.
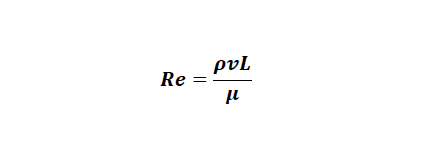
여기서 ρ는 밀도, υ는 속도, L은 특성 길이, 그리고 μ는 점도입니다. 이 무차원수의 물리적 의미는 점성력과 관성력의 비로 이해하시면 되겠습니다. 점성력이 더 큰 경우에는 유체 입자들이 서로 당기는 힘이 주요하게 작용한다는 것이고, 따라서 안정적인 유동 양상을 보입니다.
반면에 스케일이 크거나, 공기(대표적인 밀도가 낮은 유체) 보다 밀도가 높은 유체(대표적으로 물)인 경우에, 그리고 속도가 빠르면 관성이 크고, 관성이 크면 복잡한 유동 양상을 보이는 경우가 많습니다.
특히 복잡하게 굽이치는 유동, 즉 유동 방향이 주요 흐름(main stream) 방향과 반대인 영역이 발생하여 소용돌이 흐름(eddy)이 다수 발생하는 난류 유동 양상에서는 난류 해석을 위한 수치해석 모델을 사용해야 하기 때문에 레이놀즈수는 층류와 난류를 구분하는 값으로 사용되기도 합니다. 구체적으로 두 가지 상황에 따라 값의 기준이 달라집니다.
먼저 외부 유동인 경우입니다. 평판이 있고 그 위로(열린 공간으로) 유체가 흘러 갈 때, 평판과 아주 인접한 유체 입자들은 (no-slip condition에 의해서 벽면과의 거리가 0인 유체 분자는 평판과 함께 움직여서 상대 속도가 0인 조건) 속도가 느리기 때문에, 인접한 유체 입자를 잡아당겨 발생하는 점성의 영향으로 벽면으로부터의 거리에 따라서 속도 차이가 발생합니다.
이 속도 차이는 국소적인 유동 방향을 뒤틀게 되고, 최초 유동 발생 지점으로부터 멀어질수록 점차 층류에서 난류로 발달합니다. 이처럼 외부 유동(열린 공간에서의 유동)에서 난류에 대한 레이놀즈수의 기준은 약 〖Re〗_x≈500,000 입니다. 아래 첨자 x는 레이놀즈수의 정의 Re = ρvL/μ 에서 특성 길이를 의미하며, 유동이 시작되는 평판 끝으로부터의 거리를 의미합니다.
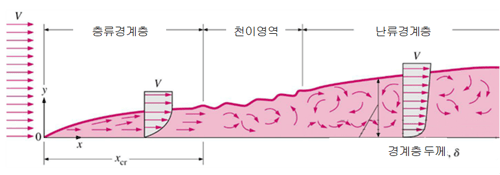
파이프 내부 유동의 경우에는 완전 발달(fully developed flow; 유동 진행 방향에 대하여 단면 유동 속도 프로파일의 변화가 없을 때) 이후에 대해서 〖Re〗_D<2300 을 층류 영역으로, 〖Re〗_D>2900 을 난류 영역으로 판단합니다. (문헌에 따라 2300과 2900 대신 다소 다른 값으로 표기하기도 합니다.)
그 사이 범위는 층류에서 난류로 점차 변화하는 천이(transitional) 영역이라고 합니다. 수치 해석 관점에서는 천이 영역을 위한 별도의 난류 모델을 사용하기보다는 편의상 단순히 대략적인 값이 2300보다 큰지 작은지를 기준으로 판단하는 경우가 많습니다.
특수한 경우로 레이놀즈수가 아주 작은 Re≪1 경우에는 Stokes’s Flow 또는 Creeping Flow라고 하며, 점성력이 지배적으로 작용하는데, Navier-Stokes equation에서 관성 항을 무시하고 계산하는 경우도 있습니다.
레이놀즈수의 대표적인 값은 아래를 참조하세요.
3. 레일리수(Rayleigh number; Ra)
레일리수는 추후 설명드릴 그라쇼프수(Gr)와 함께, 자연대류에서 층류와 난류를 구분하는 척도로 활용되는 무차원수입니다. 일반적으로 레일리수가 약 10^9보다 작으면 층류일 것으로 판단하며, 더 클 경우에는 난류의 영향을 고려해야 한다고 판단합니다.
앞서 설명한 레이놀즈수는 유동의 발생 원인이 강제적 요인(선풍기, 팬, 펌프 등)에 의하여 발생한 유동의 경우이지만, 레일리수는 유동의 발생 원인이 온도인 경우입니다.
자연 대류(natural convection; free convection)의 원리를 잠시 설명하면, 온도가 높아지면 유체 입자의 운동이 활발해져 부피가 팽창합니다. 부피가 커지면 유체의 밀도가 감소합니다. 전체 공간에 동일한 체적력(중력)이 가해졌을 때 밀도가 작은 곳에는 작은 힘이 작용하고, 밀도가 큰 곳에는 더 큰 힘이 작용합니다. 따라서 가벼운 유체는 위로 뜨고, 무거운 유체는 가라앉는데, 이 과정에서 유동이 발생합니다.
온도 차이에 의한 부력이 존재한다고 해서 반드시 자연 대류 흐름이 발생하는 것은 아닙니다. 발열체가 전체 공간의 하단에 있다면 굴뚝 연기와 같은 유동(plume)이 발생하겠지만, 발열체가 상단에 있고 밀도가 낮은 유체 또한 이미 상단에 배치되어 있다면 안정적인 상태이기 때문에 전도 열전달만이 발생하며 자연대류 흐름은 발생하지 않습니다.
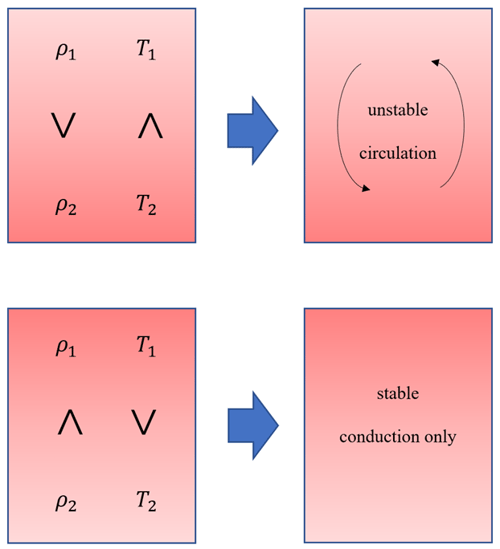
이처럼 레이놀즈수에서 밀도의 변화에 대해 별도로 고려하지 않았지만, 레일리수는 온도에 의한 밀도 변화를 고려하기 때문에 조금 복잡한 형태의 수식으로 표현됩니다.
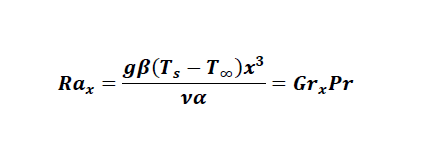
여기서〖Re〗_x는 특성 길이 x에 대한 레일리수, g는 중력가속도, β는 열팽창계수, T_s는 표면 온도, T_∞ 은 표면과 멀리 떨어진 곳의 유체 온도, ν는 동점성계수, α는 열확산계수입니다. Gr과 Pr은 그랴쇼프 수와 프란틀수며이며, 아래에서 내용을 다루고 있습니다.
물리적인 의미는 확산 열전달에 대한 시간 크기(time scale)와 대류 열전달에 대한 시간 크기의 비입니다. 추후 설명드릴 그라쇼프수와 프란틀수는 물리적 의미가 더 쉽게 와 닿는 것에 비해, 이 둘의 곱인 레일리수는 물리적 의미가 다소 어렵게 느껴질 수 있는데, 단순히 자연대류에서 층류와 난류를 구분하는 척도로써 10^9을 기준으로 판단한다는 것만 기억해도 좋겠습니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.






-1.png?width=300&name=%EB%B0%98%EB%94%94%ED%86%B5-%EC%8D%B8%EB%84%A4%EC%9D%BC_Simulation%EC%9D%B4%EA%B2%83%EC%9D%B4%EA%B6%81%EA%B8%88%ED%96%88%EB%8B%A4_696_468_-001%20(2)-1.png)










