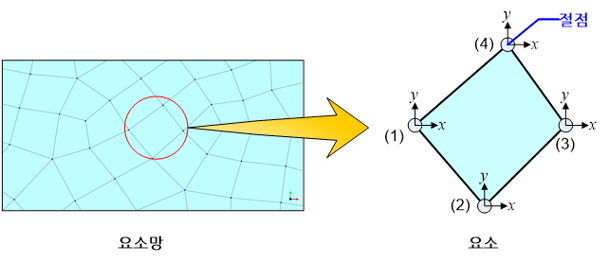
유한요소 해석(finite element analysis)에 있어 필수적인 요소망(mesh)을 구성하는 유한요소(finite element)는 물체의 형상을 유한 개로 나누어 세분화 시킨 작은 기하학적 영역 하나 하나를 일컫는다. 유한요소는 그 형상, 절점 혹은 요소 차수(element order)에 따라 구분된다. 2차원의 경우를 예를 들면, 형상에 따라 삼각형 혹은 사각형 요소로, 차수에 따라 1차, 2차 혹은 고차 요소로 구분된다. 그리고 3-, 4-, 8- 혹은 9-절점 요소로도 구분하는데, 여기서 숫자는 한 요소가 가지는 절점을 나타낸다.
절점의 개수는 요소의 차수와 관련이 있을 뿐더러 해당 요소가 가지는 자유도(degree of freedom) 혹은 미지수의 개수와도 연관이 있다. 예를 들어 1차원에 있어 1차 함수 즉 직선은 양 끝 점의 위치가 결정되면 공간 상에서 그 위치가 고정된다. 이 경우 양 끝 점의 위치는 두 개의 미지수 혹은 자유도에 해당된다.
요소에 있어 절점이란 이러한 개념으로 생각하면 이해하기 쉽다. 즉 4-절점 요소라면 각 절점에 하나의 미지수를 가지므로 총 4개의 미지수를 가지는 요소라고 생각할 수 있다(하지만 물체의 거동이 스칼라가 아닌 벡터의 경우에는 성분들을 지니고 있기 때문에 한 절점에서 벡터의 성분개수 만큼의 미지수를 가질 수 있음에 유의).
예를 들어, 4-절점 요소로 온도 분포를 계산하는 경우에는 각 절점에 하나의 온도 값을 미지수로 하기 때문에 이 요소는 총 4개의 미지수를 갖는다. 하지만 4-절점 요소로 2차원 속도 분포를 계산하는 경우에는 각 절점에서 x 및 y방향 속도 성분을 미지수로 가지므로 이 요소는 총 8개의 미지수를 가진다.
요소망 내 인접한 요소들은 같은 위치에 있는 절점들을 서로 공유한다. 이를 통해서 요소망 내 모든 요소들은 서로 연결되어 하나의 유기적인 네트워크를 형성하게 된다. > 절점 더 자세히 보기🔎