자연계에서 발생하는 현상을 재현하는 방법으로 크게 실험적인 방법과 수치해석(numerical analysis)적인 방법으로 분류할 수 있다. 전자의 경우에는 축소모형과 실험장치를 만들어야 하고 후자의 경우에는 그 현상을 지배하는 수학적인 표현과 관련 조건들을 유도하여야 한다. 이러한 과정을 총칭하여 모델링(modeling)이라고 부른다. 흔히 컴퓨터 화면상에 물체의 형상을 가시화 하는 것을 모델링의 전부라고 생각하는데 이것은 모델링의 단편적인 일부에 해당된다.
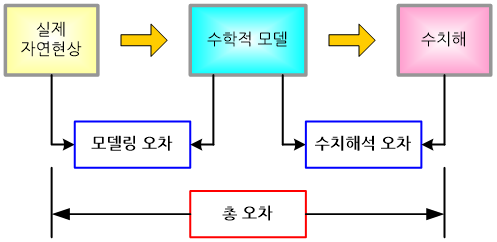
모델링 오차라 함은 자연계의 실제 현상과 실험모델 혹은 수학적으로 표현되는 모델 사이의 차이로 정의된다. 예를 들어, 비행중인 항공기 주위의 공기흐름을 재현하기 위해 풍동실험을 하는 경우, 실제상의 무한한 공기 영역을 실험적으로 구현을 할 수 없는 한계를 포함하여 갖가지 제약조건들이 수반된다. 한편 수학적인 표현에 있어서는 공기의 흐름을 지배하는 미분방정식과 조건들을 유도하는 과정에서 갖가지 가정(assumption)과 불확실성이 수반되기 마련이다. 이러한 한계성, 가정 그리고 불확실성 등이 모델링 오차의 원인이 된다.
유한요소 해석에서 흔히 말하는 오차(error)는 위에서 말한 모델을 수치해석적으로 푸는 과정에서 컴퓨터 성능의 한계와 수치해석 기법상의 한계에 기인한 수치해석 오차(numerical error)로서 모델링 오차와 구분되어야 한다. 그리고 가장 중요한 사항은 엄밀한 의미에서 오차는 모델링 오차와 수치해석 오차를 합한 값이라는 점이다. 또한 수치해석의 궁극적인 목표는 수치해석 오차만을 최소화 시키는 것이 아니라 실제 자연 현상을 얼마나 정확하게 재현하느냐에 초점이 맞혀져야 한다. 다시 말해, 수치해석 오차뿐만 아니라 모델링 오차도 동일하게 최소화 되어야 한다는 말이다.
아무리 좋은 컴퓨터와 소프트웨어를 사용하여 유한요소 해석을 수행하더라도 수치해석을 위한 모델이 적합하지 않으면 실제 자연현상과는 전형 다른 엉뚱한 문제를 푸는 것에 불과하기 때문이다.
.