자연형상에 대한 수치 시뮬레이션을 위하여 가장 많이 사용되고 있는 유한요소법(finite element method)의 가장 큰 특징이자 장점은 근사해(approximate solution)를 표현하기 위해 사용되는 보간함수(interpolation function)를 요소망(mesh)을 이용하여 체계적으로 정의할 수 있다는 점이다.
그런데 요소망 내 각각의 요소(element)와 절점(node)은 상호간에 유기적인 연결성(connectivity)을 항상 유지해야 하는데, 이러한 조건을 만족시키는 요소망을 생성하는데 소요되는 시간은 물체의 형상이 대형화 되고 복잡해질수록 기하급수적으로 증가한다. 하나의 유한요소 해석 작업에 소요되는 총 해석시간의 대부분이 요소망 생성에 할당된다고 하여도 과언은 아니다.
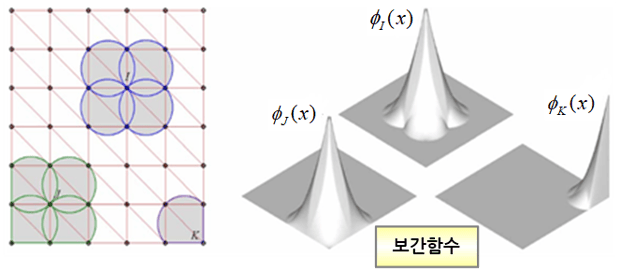
이와 같은 요소망 생성이 안고 있는 본질적인 단점을 해결하고자 탄생된 수치해석 기법이 바로 무요소기법이다. 무요소기법에서는 대상 물체의 기하학적 영역을 여러 개의 작은 영역들로 세분화 시키지 않고, 영역 내에 유한개의 점들을 흩뿌리고 각각의 점을 중심점으로 한 보간함수들을 정의하여 근사해를 표현한다. 각 점에 대한 보간함수는 해당 점을 중심으로 작은 영영 내에서만 정의되는데, 중요한 사항은 각각의 작은 영역들은 유한요소(finite element)와 같이 정확히 접해야 할 필요는 없다는 점이다.
물론 유한요소와 같이 각 점을 중심으로 한 작은 영역들의 조합은 대상 물체의 기하학적 영역을 완전히 채워야 하지만, 유한요소법에서와 같이 엄격한 연결성이나 접합성을 필요로 하지는 않는다는 장점을 지니고 있다. 하지만, 무요소법이 안고 있는 가장 큰 난점은 행렬을 유도하기 위한 수치적분(numerical integration)과 변위 경계조건의 적용이다.
이러한 문제를 해결하기 위해 여러가지 추가적인 기법들이 소개되었지만, 궁극적으로 기존의 유한요소법에서의 요소망과 가우스 구적법(Gauss quadrature rule)을 활용한 수치적분을 사용하고 있으며 벌칙기법(penalty method)과 같은 기존의 기법들을 채택하고 있다. 더욱이 3차원 문제나 형상이 복잡하고 대형인 경우, 물체 내에 흩뿌려진 점들과 이에 해당하는 보간함수를 체계적으로 생성하기가 어려운 문제에 직면하고 있다. > 무요소법 더 자세히 보기🔎