아무리 작은 물체라고 하더라도 어느 정도의 체적을 갖는 3차원(three dimension) 형상으로 되어 있다. 하지만 물체가 길이에 비해 나머지 두 방향으로의 크기가 상대적으로 작은 경우에는 특징적인 물체 거동을 나타낸다. 예를 들어 축 방향으로의 길이에 비해 단면적이 상대적으로 작은 가느다란 막대를 굽히는 경우를 생각해 보자. 굽힘(bending)에 따른 막대의 전체적인 변형 형상(deformed shape)은 막대 중심축의 변형 형상과 거의 일치한다.
다시 말해, 변형 후 막대의 곡률반경은 중심축에서나 막대의 안 그리고 바깥 면에서 거의 동일하다. 그리고 중심축과 막대 테두리에서의 변형, 변형률(strain) 그리고 응력(stress)의 차이는 선형적으로 가정할 수 있다. 이러한 기하학적 그리고 거동적 특징을 나타내는 물체는 박판 구조물(thin-walled structure)의 일종으로 취급된다. 그리고, 유한요소 해석(finite element analysis)을 위한 요소망(mesh) 생성에 있어 3차원 요소를 사용하지 않고 단지 중심축을 유한 개의 선 요소를 사용하여 세분화 시킨다.
그 결과 물체의 기하학적 형상은 3차원일지라도 요소망 자체는 1차원으로 표현된다. 그리고 막대의 두께, 단면정보 그리고 두께 방향으로의 선형적 변위(displacement)는 미리 계산되어 강성행렬(stiffness matrix)과 질량행렬(mass matrix)에 반영된다. 그리고 계산결과를 토대로 두께 방향으로의 거동의 변화는 중심축의 거동 값과 선형적 가정을 이용하여 구할 수 있다.
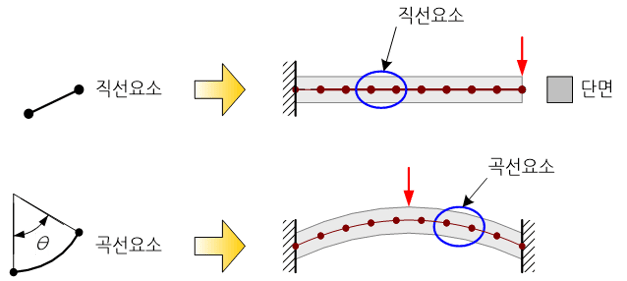
선 요소에는 형상적인 측면에서 직선과 곡선 요소로 나눌 수 있고, 절점의 자유도에 따라 보 요소(beam element), 봉 요소(rod element), 링크요소(link element), 강체 요소(rigid element)로 구분된다.
.