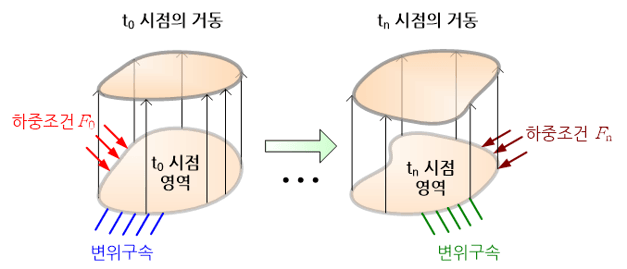
임의 물체를 특정한 속도로 발사하였을 경우, 이 물체의 시간에 따른 궤적, 날아간 거리 그리고 목표지점에 도달하기까지 걸린 시간을 풀어본 경험이 있을 것이다. 이와 같이 시간에 따른 물체의 거동을 구하는 것을 초기치 문제를 푼다고 한다.
초기치란 이름이 붙게 된 이유는 시간에 따른 물체의 거동이 초기 발사지점, 발사각도 및 발사속도와 같은 초기조건(initial condition)에 절대적으로 영향을 받기 때문이다. 경계치 문제(boundary value problem)의 거동이 외부와 직접 접촉하는 물체의 경계(boundary)에서의 구속 및 하중조건에 의해 결정되는 것과 동일한 맥락이다.
또한 경계치 문제의 수학적 표현 속에 물체 거동의 위치에 따른 변화율을 포함하는 반면, 초기치 문제의 수학적 표현 속에는 거동의 시간에 따른 변화율을 포함하고 있다. 예를 들어 발사된 물체의 위치에 대한 시간 변화율은 물체의 속도가 되고, 이 속도의 시간에 대한 변화율은 가속도가 된다. 경계치 문제에 있어 거동의 위치에 따른 변화율은 거동을 근사화 시키는 보간함수(interpolation function)를 위치에 대해 미분하면 된다.
하지만 초기치 문제에 있어 거동의 시간에 대한 변화율은 보간함수의 직접적인 미분이 아닌 특별한 수치적 미분을 적용해야 한다. 시간에 대한 변화율을 계산하는 가장 간단한 방법은 인접한 두 시점에서의 거동의 차이를 두 시점 사이의 시간 간격(time step)으로 나눈 기울기로 대체하는 것이다.
이러한 방식으로 거동의 시간에 대한 변화율은 전 후 시점에서의 거동값들로 대체되어 표현된다. 그리고 초기시점에서 부터 원하는 시점까지의 물체 거동은 이렇게 대체 표현된 수학적 표현을 초기값을 이용하여 반복계산을 통해 계산된다. 이렇게 초기치 문제의 거동을 시간에 따른 반복계산을 통하여 구하는 수치적 방법을 특별히 시간적분(time integration)이라고 부른다.
.