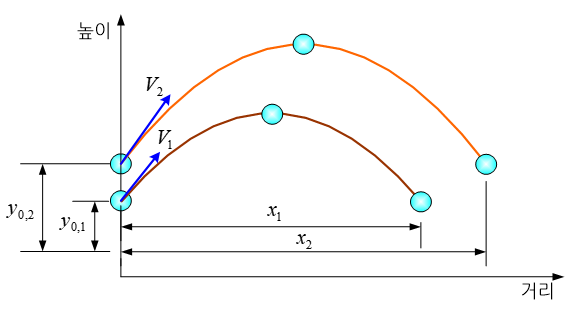
돌을 세게 던지면 보다 멀리 날아간다는 사실은 누구나 익히 알고 있는 사실이다. 그리고 일정한 질량을 가지고 있는 돌을 던졌을 때 날아가는 거리를 계산하기 위해서는 돌의 운동을 표현하는 운동방정식을 풀어야 한다.
물체의 운동방정식은 물체의 공간상의 위치에 대한 2차 시간 미분으로 표현되며, 시간에 대해 2번 적분해야 한다. 수학적인 정의로부터 2차 미분방정식을 2번 적분하게 되면 2개의 적분상수가 나오게 되며, 이 적분상수를 결정하여야 하나의 해답을 구할 수 있다.
이 경우, 적분상수를 결정하기 위해 사용되는 조건이 바로 초기조건에 해당된다. 위 문제의 경우, 2개의 초기조건은 각각 돌의 초기위치와 초기속도가 된다. 일반적으로 n차 미분방정식인 경우 초기조건은 n개가 되며 (n-1)차 미분까지 변수들의 초기 시점에서의 값으로 정의된다.
참고로 이와 같이 물체의 거동이 시간에 따라 변화하고 초기조건에 의해 하나의 해답이 결정되는 문제를 초기치 문제(initial value problem)라고 부른다. 초기치 문제와 구분되는 문제로 경계치 문제(boundary value problem)가 있으며, 이 문제의 해답은 물체 경계(boundary)에서의 경계조건(boundary condition)이라 불리는 구속조건에 의해 결정된다.
그리고 물체의 거동이 시간과 공간 좌표 모두에 의해 표현되며, 초기 및 경계조건에 의해 하나의 해답이 결정되는 문제를 초기치-경계치 문제(initial and boundary value problem)라고 부르며, 거의 대부분의 동해석(dynamic analysis) 문제들은 이 유형에 속한다.
.