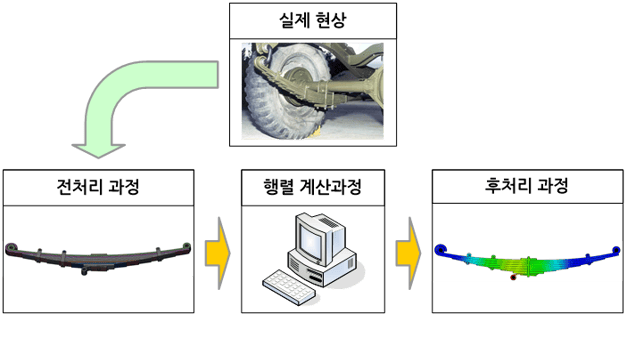
자연계에서 발생하는 현상이나 물체의 거동을 분석(계산)하는 방법에는 크게 세가지가 있다. 첫째는 실제 상황을 실험적인 방법으로 재현하는 것이고, 다음으로는 수학적인 표현으로 바꾸어 이론적인 해답을 푸는 것이다. 전자와 후자는 각각 장단점을 지니고 있다. 특히 후자의 경우는 대상 물체의 기하학적인 복잡성 때문에 실제 문제에 적용하기에는 많은 한계가 있다.
이 한계를 극복하기 위한 방법이 컴퓨터를 활용한 수치해석(numerical analysis) 기법이다. 수치해석 기법에는 많은 종류가 있지만 공통적인 특징은 수학적인 표현(거의 대부분 미분방정식)을 행렬식으로 변환하여 근사적인 해답을 구하는 것이다. 수치해석 기법의 종류는 근사해(approximate solution)를 구하기 위해 필요로 하는 보간함수(interpolation function)를 어떻게 정의하느냐에 따라 분류된다.
수치해석 기법 중에서 가장 보편적으로 사용되는 유한요소법(finite element method)은 보간함수를 유한요소(finite element)를 이용하여 매우 편리하고 체계적으로 정의한다. 보간함수의 정의 외에도 유한요소 해석이 가장 보편적으로 사용되는 이유는 자연계에서 발생하는 어떠한 현상이라도 수학적 표현식만 주어진다면 적용이 가능하다는 점이다. 컴퓨터의 급속한 발전과 수치해석 및 모델링 기술의 발전에 힘입어 유한요소 해석은 공학 및 자연과학 분야에만 국한되지 않고 학문 전 분야로 확산되고 있는 추세이다.
.