유한요소 해석을 위해 대상이 되는 물체의 기하학적 영역을 여러 개의 작은 세부 영역들로 쪼개는 작업을 요소망(mesh)을 생성한다고 말한다. 그리고 각각의 세부 영역들을 유한요소(finite element)라고 부르는데, 이와 같이 요소망을 생성하는 이유는 구하고자 하는 물체의 거동을 근사하기 위해 사용되는 기저함수(basis function)를 아무리 물체의 형상이 복잡하더라도 체계적이고 효과적으로 정의하기 위함이다. 그리고 유한요소법이라는 이름이 붙여지게 된 근원이 바로 여기에 있다.
각각의 요소는 절점(node)이라 불리는 특정한 점들을 가지고 있는데, 이 절점들에서 물체의 거동값을 계산하여 요소망 전체에 걸친 거동의 전체 분포를 최종적으로 표현(근사)한다. 한편, 각 절점에서의 물체의 거동값은 물체 거동을 계산하기 위해 수치적으로 변환시킨 행렬 방정식의 미지수, 즉 자유도(degree of freedom)에 해당된다.
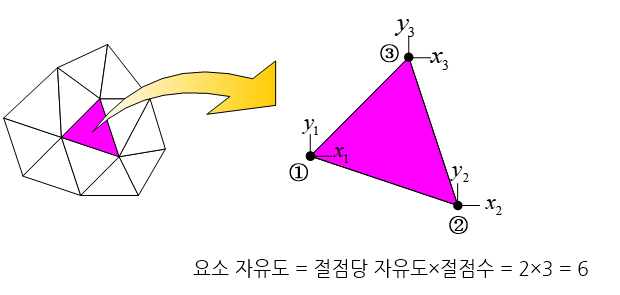
한 절점이 가지게 되는 미지수의 개수를 절점 자유도(nodal degree of freedom)라고 부르며, 풀고자 하는 물체 거동의 유형에 따라 달라진다. 요소 자유도란 한 요소내 각 절점에서의 자유도를 모두 합한 자유도를 의미한다. 예를 들어 절점 자유도가 3인 4개의 절점으로 구성되어 있는 사각형 요소의 요소 자유도는 12가 된다.
.