우리 주위에서 흔히 볼 수 있는 물체의 거동은 물체 내 위치에 따라 그 거동이 변할 뿐만 아니라 시간과 더불어 변하는 경우가 많다. 시간과 무관하게 물체 내 공간상의 위치에 따른 거동을 분석하는 경우를 경계치 문제, 그리고 물체 내 일정한 지점에서 시간에 따라 변하는 물체의 거동을 분석하는 것을 초기치 문제(initial value problem)로 구분하고 있다. 하지만 자연계 대부분의 현상은 그 거동이 공간상의 위치뿐만 아니라 동시에 시간에 따라서도 변하기 때문에 경계치-초기치 문제(boundary and initial value problem)로 볼 수 있다.
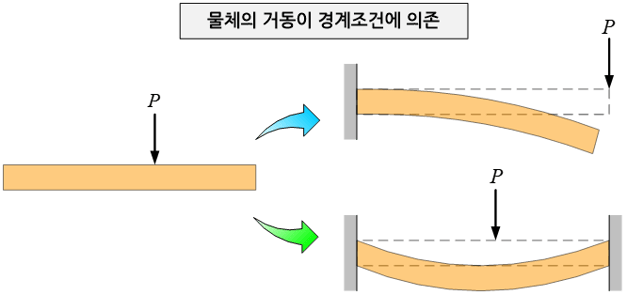
예를 들어, 고층건물이 자체 무게에 의해 얼마나 큰 응력(stress)이 내부에 발생하는가 하는 문제는 경계치 문제에 해당되고, 고층건물 내 특정한 부위가 지진파에 따라 시간적으로 어떻게 거동할 것인가는 초기치 문제에 해당된다. 그리고 지진파에 따라 고층건물 전체의 변형이나 응력이 시간과 더불어 어떠한 변동을 나타내는가 하는 문제는 경계치-초기치 문제에 해당된다. 시간과 무관하게 물체 내 위치에 따른 거동을 분석하는 것을 경계치 문제라고 부르는 이유는, 물체 내 거동이 물체의 경계, 즉 외부와 직접 접하고 있는 물체의 표면에 가해지는 각종 구속조건과 경계조건(총칭하여 경계조건(boundary condition)이라 부름)에 의해 절대적으로 좌우되기 때문이다. 예를 들어 한 쪽 끝 단이 벽에 고정되어 있는 가느다란 나무막대를 생각해 보자. 다른 쪽 끝 단에 수직하중을 가하는 경우와 다른 한 쪽 끝 단도 동시에 지지하면서 막대의 가운데에 수직하중을 가하는 두 경우에 있어서 막대가 변형(deformation)되는 모양은 판이하게 다르다.
이처럼 경계치 문제에 해당되는 물체의 거동은 경계조건에 주도적인 영향을 받는다. 따라서, 이러한 문제를 유한요소 해석(finite element analysis)으로 풀고자 할 경우, 해석결과의 신뢰성은 경계조건을 얼마나 정확하게 반영하느냐에 달려있다고 하여도 과언은 아니다.
.