진공 해석을 위한 기초 이론
목차
1. 연속체(Continuum)
2. 희박기체(Rarefied gas)
3. 크누센 수(Knudsen number)
4. 절대압력과 상대압력
진공 상태를 해석하기 위해서는 사전에 검토해야 할 부분이 있습니다. 똑같이 진공이라는 표현을 사용하더라도 전산유체역학 관점에서는 경우에 따라 물리적 의미가 다를 수 있습니다.

예를 들어 일상 생활에서 대기압보다 약간 낮은 수준의 음압 환경이면 모두 진공이란 표현을 쓰는 사람이 있을 수 있고, 어떤 사람은 펌프 석션을 통해서 챔버 내부 유체를 빨아들이는 환경이면 ‘진공 상태를 만든다’고 표현할 수도 있습니다. 또한 사전적 의미 그대로, 어떤 공간 내부에 유체가 거의 없는 진공 상황에 대한 해석을 원할 수도 있습니다.

이번 시간에는 유체역학 및 CFD 관점에서 진공을 어떤 식으로 분류하는지, 압력 설정을 어떤 식으로 해야 하는지 알아보겠습니다.
1. 연속체(Continuum)
진공의 정도를 어떻게 분류하는지 알기 위해서는 먼저 연속체에 대한 이해가 필요합니다. 유체의 움직임을 미시적 관점으로 봤을 때, 유체 분자 A가 외력에 의해서 움직이면 이웃한 분자 B와 충돌을 하며 운동에너지를 전달하게 됩니다. 수조에 물을 받아 놓은 후 한쪽 끝에 물방울이 떨어지면 잔잔한 물결이 전파되는 것, 부채질을 하면 부채 표면으로부터 유체 분자들이 밀려 나와 바람을 일으키는 것은 유체 분자들이 그만큼 서로 영향을 줄 만큼 가까이 있기 때문입니다.
이처럼 유체 분자들이 특정 공간 내에 충분히 많은 경우, 에너지 전달을 할 만큼 가까이 있는 경우를 ‘연속체(continuum)’라고 합니다. 일상 생활을 떠올렸을 때 이러한 현상들은 간단하면서도 당연한 내용이지만 이 사실은 유체 역학 및 해석 관점에서 매우 중요하게 작용합니다.
이전 포스팅에서 다루었던 라그랑지 기술법(Lagrangian description) 및 오일러 기술법(Eulerian description)과도 관련이 있는데요, 모든 유체 입자 하나 하나를 추적하는 해석 방식이 아니라, 관심을 갖는 공간을 기준으로 유체의 움직임을 해석할 수 있는 것은 이 연속체 개념 덕분입니다. 개별적인 유체 분자의 움직임을 일일이 추적하는 해석은 현실적으로 불가능합니다.
이전 포스팅이 궁금하다면?
아래 그림을 클릭!👇
하지만 연속체 개념을 적용하면 수많은 유체 분자의 물리적 특성을 특정 체적에 대하여 평균화하여 계산할 수 있으며, 유체 해석에 필요한 방정식을 풀이하는 것이 훨씬 편리해지기 때문입니다. 이렇게 유체를 연속체로 가정한 풀이 방법이 합당할까요?
답은 ‘그렇다’입니다. 실제로 유체 분자 사이의 거리가 매우 작기 때문인데요, 일상의 압력과 상온에서 기체 분자의 간격은 10^(-6) mm 수준이고, 액체는 10^(-7) mm 수준입니다. 또한 1 세제곱 밀리미터의 육면체(지금 손으로 그 크기를 가늠해 보세요)에 있는 유체 분자의 수는 기체가 10^18 오더(order)이고, 액체는 10^21 정도입니다.

2. 희박기체(Rarefied gas)
대부분의 일반유동 해석은 앞서 설명한 것처럼 연속체 상황이기 때문에, 기존의 고전적인 풀이 방식대로 접근할 수 있습니다. 하지만 진공의 정도가 커지면 상황은 달라집니다. 희박 기체 유동이란, 시스템 내 분자간 거리가 충분히 멀어서 운동량 및 에너지 전달이 연속적이지 않은 유동을 말합니다.
압력이 굉장히 낮은 저압 펌프나 초고층/고산 지대의 대기 유동, 아주 작은 소형 유체 장치에서는 연속체가 아니라 희박 기체의 특성을 보이게 됩니다. 유체 분자가 서로 충돌하기 이전의 이동 거리인 평균 자유 경로(mean free path)가 보통의 상황보다 훨씬 큰 경우인데, 이 때는 물리량의 전달이 도미노처럼 연속적이지 않아서 일반적인 유체 해석을 위한 지배방정식으로는 풀이가 불가능합니다.
그렇다면 연속체와 희박기체를 구분하는 정량적 기준이 있을까요? 네, 아래에서 설명하는 크누센 수를 통해서 분류할 수 있습니다.
3. 크누센 수(Knudsen number)
크누센 수는 유체의 진공 정도를 구분할 수 있는 무차원 수입니다. 보통은 진공 챔버나 전자기기처럼 해석하는 물체의 길이가 분자의 이동 거리보다 훨씬 크기 때문에 크누센 수는 아주 작은 값을 갖게 되며, 이 때는 앞서 말씀드린 연속체로 가정한 유체 해석이 가능합니다. 하지만 그 둘의 길이 스케일이 비슷하다면, 연속체로 가정하는 것은 적합하지 않으며 크누센 수가 1과 비슷하거나 더 큰 경우에는 통계학 관점에서 접근해야 합니다.
다시 한 번 공학적으로 크누센 수를 정의하면, 유체 분자의 평균 자유 경로(mean free path)와 특성 길이(characteristic length)의 비로, 아래와 같이 나타낼 수 있습니다.
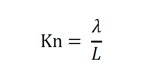
온도와 압력 조건, 그리고 유체 분자의 직경을 알면 평균 자유 경로를 계산할 수 있습니다.
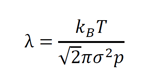
대입하면 크누센 수는 다시 아래와 같이 나타낼 수 있습니다.
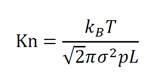
여기서 k_B는 볼츠만 상수(Boltzmann’s constant; 1.38×10^(-23)J/K), T는 절대온도, σ는 유체 분자의 직경, p는 절대압력, L은 특성 길이입니다.
문헌에 따라 진공 정도를 분류하는 크누센 수의 기준 값에 약간의 차이가 있기도 하지만, 일반적으로 아래와 같이 연속체와 희박 기체를 분류할 수 있습니다.
|
Kn < 0.01 |
Continuum flow |
연속체 |
|
0.01 < Kn < 0.1 |
Slip flow |
희박 기체 (Rarefied gas) |
|
0.1 < Kn < 10 |
Transitional flow |
|
|
Kn > 10 |
Free molecular flow |
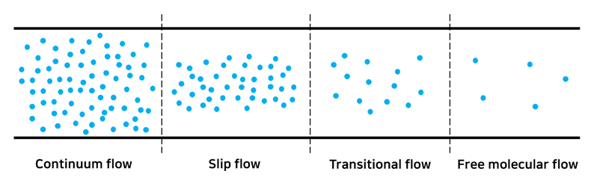
- Continuum flow : 분자간 운동량 및 에너지 전달이 연속적으로 작용함.
- Slip flow : 벽면 근처에서 희박하여 운동량 및 에너지 전달이 연속적이지 않지만, slip wall로 근사 가능. 그 이외 영역에서는 연속성 유체의 특성을 보임.
- Transitional flow : 전 영역에서 희박기체 특성이 나타남. Navier-Stokes equation 대신 수정된 Boltzmann equation 사용 필요.
- Free molecular flow : 매우 희박한 유동으로, 분자간 충돌 무시 가능함. 유체 분자들의 벽면 충돌은 확률통계적 관점에서 접근 필요.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.


















