지진이나, 바람, 파도와 같은 경우에는 어떤 시간에 측정해서 그 시간에 대한 어떤 하중을 알아냈다 하더라도 다음 시간에 가면 동일한 하중이 작용하지 않습니다. 그래서 이렇게 정형화된 하중으로 표현을 할 필요도 없고, 할 수도 없는 그런 경우에 어떻게 해석을 할 수 있을까요?
이 랜덤 진동 해석은 그런 하중을 정형화된 시간의 함수가 아니라 좀 확률적으로 접근해 보면 어떨까 하는 발상에서 등장했습니다. 이 시간 대의 바람의 크기나 방향이 다음 시간 대의 바람과 크기나 방향이 같지는 않지만, 일정한 시간 동안 그 바람에 데이터를 모아보면 전체적으로는 같은 거동을 보인다는 가정을 할 수 있습니다. 평균이 같거나, 표준 편차가 같은 식으로 접근 할 수 있는 방법이 없을까 하는 아이디어가 랜덤 진동 해석입니다.
목차
1. 랜덤 프로세스
2. 확률적 접근 방법
3. 스팩트럼 밀도 함수
4. 랜덤 진동 응답
5. 랜덤 진동에 의한 피로 파괴
1. 랜덤 프로세스
어떤 한 시간 축에서 제가 바람을 한 번 측정해봤습니다. 시간에 따라서 바람이 이렇게 나오면 그 다음 날 와서 또 제가 또 한 번 측정을 또 했습니다. 그래서 이 축을 시간 축에 반복되는 것들을 특별한 용어로 앙상블이라고 합니다. 어떤 시간에 대한 함수들의 샘플입니다. 그것을 저희는 랜덤 프로세스라고 합니다. 시간 축으로 봐도 랜덤하고, 샘플(앙상블) 축으로 봐도 랜덤합니다.

그런 데이터를 랜덤 프로세스라고 부릅니다. 시간을 정해 놓고 보면 t1이라는 시간에서 샘플을 쭉 모아 놓으면 샘플이 다 다르겠죠. 특정 시간에서 그 샘플을 다 모아 놓고 히스토그램을 그리면 특정한 분포를 보이고 그 분포를 저희들이 확률 밀도 함수로 피팅하면 확률 밀도 함수로, 확률로 주어지는 주어진 시간에서 샘플들이 확률 분포를 보이는 그런 과정입니다.
시간이 바뀌면 또 다른 확률 분포를 보이겠죠. 그래서 주어진 시간에서 데이터들이 이제 확률 분포로 나타나는 그런 것을 이제 랜덤 프로세스라고 합니다.
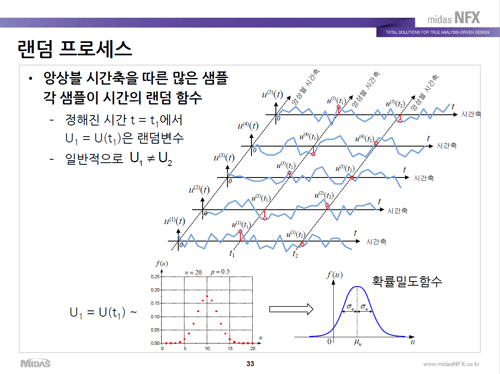
이런 해석들을 유한 요소법으로 구현하고 각 시간 별로 해석 결과를 찾아서 프로세스화 하기에는 굉장히 많은 데이터와 시간이 소요됩니다. 사람들은 좀 더 쉽게 표현하기 위해서 이것을 정상 프로세스라는 가정을 했습니다.
•
•
•
3. 스펙트럼 밀도 함수
영어로 하면 Power spectral density라고 하는데요. Power라는 말이 나온 것이 전기 공학에서 시작되기 때문에 u가 사실은 전류였습니다. 이 이론은 전류와 전력을 계산하기 위해 생겼기 때문입니다. Power spectral density라고 이름이 붙었는데 랜덤 프로세스의 제곱(분산)의 주파수 영역에서의 표현이라고 보시면 되겠습니다.
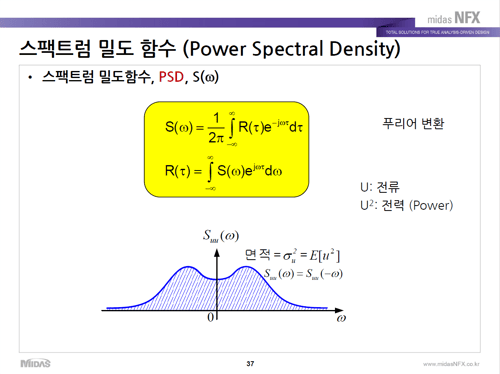
이 Power spectral density가, 스펙트럼 밀도 함수가 랜덤 진동 해석에서는 Input(입력값)입니다. 랜덤하게 들어오는 어떤 하중의 데이터를 저희들이 각 시간에 대한 함수로 표현하는 것이 아니라 주파수 영역에서 밀도로 표현하는 것입니다. 특정한 주파수에서 이 하중이 많이 있으면 Density(밀도)가 올라가는 것입니다.
특정한 주파수 영역에 해당 주파수가 없으면 Density가 떨어지는 것이고 그런 식으로 주파수 영역에서 밀도가 얼만큼인지, 그 하중의 밀도가 얼만큼 된다는 것을 통계학적으로 표현하고 이것을 Input으로 해서 Output(결과)도 이런 Form으로 풀려고 하는 것이 랜덤 진동 해석입니다. 개별적인 하중을 따라가는 것이 아니고 주파수 영역에서 그 하중의, Frequency에서 밀도가 얼만큼 될 것이냐, 출력도 응력이면 응력의 밀도가 확률적으로 얼만큼 될 것이냐 하는 것을 계산하는 것이 랜덤 진동 해석의 특성입니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
















