이번 강의 주제는 '미세조직과 재료 물성의 상관관계'입니다. 정확한 해석 결과를 얻기 위해서 설계자는 본인이 사용하는 재료의 특징을 정확히 이해하고 있어야만 합니다. 특히 재료의 비선형 거동을 고려하는 경우에는 이론적인 접근뿐만 아니라 실험을 통한 재료 파악이 함께 필요합니다. 이번 강의를 통해 다양한 결정 구조에 따라 재료의 비선형 물성치를 어떻게 정의할 수 있는지, 선형/비선형 재료 모델의 특징은 무엇인지에 대해서 알아보시길 바랍니다.
목차
1. Elasticity : Linear and Nonlinear
2. Case Study : Vanadium
3. Case Study : Rubbers
1. Elasticity : Linear and Nonlinear
일반적으로 재료의 거동에 대해 정의할 때 우리는 Stress-Strain Curve(응력-변형률 곡선)를 통해 표현하고, 원자 간의 위치 에너지(Potential energy)를 2차 함수로 표현하여 평형 상태에서의 에너지와 변형 이후의 에너지를 정의합니다. 하지만 위와 같은 수식에서는 재료의 거동을 탄성 범위의 선형 거동에 대해서만 정의하고 있기 때문에 온도 변화를 비롯한 비선형 거동에 대해서는 표현할 수 없다는 한계를 가지고 있습니다.
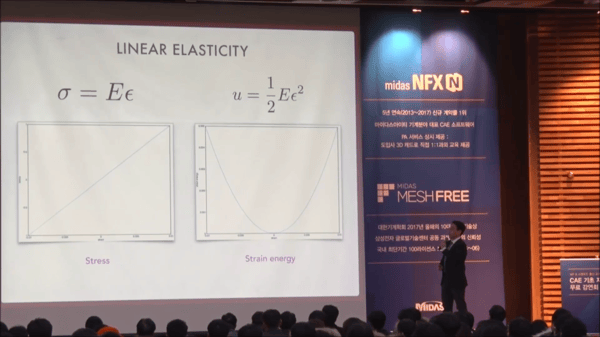
이런 문제를 해결하기 위해 변형식을 만드는 방식으로 계산을 수행하고 있지만 근본적인 문제가 있기 때문에 선형 모델을 통해서는 재료의 항복(Yielding), 열팽창(Thermal expansion), 상변화(Melting), 온도 의존성(Temperature dependence)을 고려할 수 없습니다.

위와 같은 문제에 대한 근본적인 해결책을 찾기 위해 분자 결합 에너지(Binding energy) 곡선을 CAE에 적용하는 방법을 찾고 있으며 앞서 확인했던 포물선 형태의 위치 에너지 함수보다 정확도를 높일 수 있기 때문에 높은 활용성이 예상됩니다. 아래 보이는 그래프는 원자 간의 거리에 따른 위치 에너지를 나타낸 모습입니다.
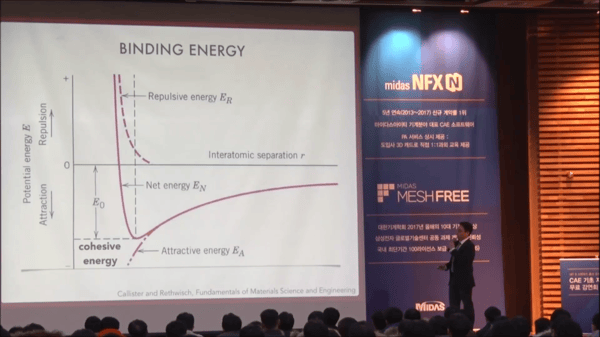
FEM 해석을 수행하는 엔지니어에게 재료의 비선형 거동은 복잡하고 어려운 문제로 느껴집니다. 공학도(Engineer)는 선형(Linear) 거동에 대한 수식과 내용을 먼저 학습했기 때문에 비선형 거동은 선형 거동에서 확장된 개념이라고 느끼기 쉽습니다. 하지만 모든 자연 현상은 비선형(Nonlinear)으로 구성되어 있고 계산을 용이하게 만들기 위한 방식으로 선형화된 수학적 모델을 만들게 됩니다. 따라서, 비선형으로 구성된 자연 현상에 대한 기본 개념을 이해하고 선형화된 표현을 접하는 방식으로 접근하면 어렵게만 느껴지던 문제에 대해 쉽게 접근할 수 있는 경우가 많습니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
















