유체는 액체(Liquid), 기체(Gas)와 같이 고체와는 다르게 그 모양이 정해지지 않고 흐르는 물질을 말합니다. 이러한 유체는 밀도(Density)와 점성(Viscosity), 표면장력(Surface tension)이라는 3가지 대표적인 성질을 가지고 있습니다.
목차
Part 1. 유체역학 기초
Part 2. 전산유체역학(CFD)
Part 3. 폐 유동 해석
Part 4. 2상 유동 해석
Part 1. 유체역학 기초
밀도는 단위부피당 얼마나 무거운지를 나타냅니다. 무거운 유체는 밑으로 가라앉고, 가벼운 유체는 위로 뜨게 됩니다. 이처럼 중력은 유체의 위치를 결정하는 변수로 작용합니다.
점성은 유체가 움직이는 상황에서 벽면이 유체를 잡아당기는 힘을 나타내는 변수로써 이로 인해 벽면으로부터 떨어진 거리에 따른 유체 속도의 구배가 발생하고, 속도 구배에 점성을 곱해서 전단응력을 계산할 수 있습니다. 이 전단응력에 면적을 곱하면 마찰력이 됩니다. 즉, 점성은 유체의 흐름에 대한 저항을 계산하는데 중요한 변수로 작용합니다.
표면장력은 모세관 현상을 설명할 수 있는 계수입니다. 빨대 안의 유체 표면을 자세히 보면, 가장자리가 살짝 올라간 것을 볼 수 있습니다. 표면장력은 서로 다른 두 유체 간의 잡아당김의 정도를 결정해서 유체의 표면 모양을 결정합니다.

Part 1에서는 위의 내용 이외에도 층류(Laminar flow)와 난류(Turbulent flow)에 대한 구분, 유동 현상을 결정하는 레이놀즈 수(Reynolds number), 프루드 수(Froude number), 웨버 수(Weber number), 본드 수(Bond number)에 대해 소개합니다.
Part 2. 전산유체역학(CFD)
흐르는 유체의 정보를 알기 위해 우리는 나비에 스톡스 방정식의 해를 얻어야 합니다. 하지만, 매우 단순한 형상의 관을 따라 흐르는 유체이면서 일부 변수에 대한 영향을 무시한다는 가정을 하지 않는 경우에는, 방정식의 해를 손으로 풀기 매우 어렵거나 불가능에 가깝습니다.
따라서 경우 실험적인 접근을 제외한다면 컴퓨터의 계산 능력에 의지할 수 밖에 없습니다.

이런 문제를 해결하기 위해 전산유체역학(CFD)은 다양한 방식으로 발전하고 있습니다. 컴퓨터가 위와 같은 편미분방정식에 대한 해를 얻기 위해서는 아래와 같은 방법이 사용됩니다.
유한차분법(FDM, Finite Difference Method), 유한체적접(FVM, Finite Volume Method), 유한요소법(Finite Element Method)은 모두 나비에 스톡스 방정식의 해를 얻기 위해 컴퓨터가 풀 수 있는 형태로 방정식을 변환하는 이산화 과정을 거친다는 공통점을 가지고 있으나 각 방식 별 특징이 존재합니다.
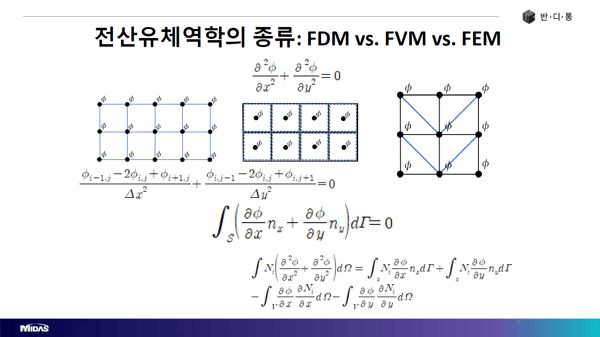
Part 2에서는 이외에도 Q1Q1(P1P1)과 Q2Q1 요소 기법의 장단점, CFD 계산 알고리즘에 대해 소개합니다.
Part 3. 폐 유동 해석
전산유체역학(CFD)는 현재 수많은 산업 분야에서 활발히 사용되고 있습니다. 아래 그림은 인간의 기관지와 폐로 흡입되는 공기의 흐름을 파악하는 해석 결과입니다.
CFD의 장점은 보이는 것과 같이 실험이 불가능 또는 매우 어려운 현상에 대해서도 쉽게 해를 얻을 수 있으며, 계측 장비가 설치되지 않은 구조물 또는 현상에 대해서도 해석을 수행한 대상에 대해서 모든 위치에서 물리량 결과를 얻을 수 있다는 점입니다.
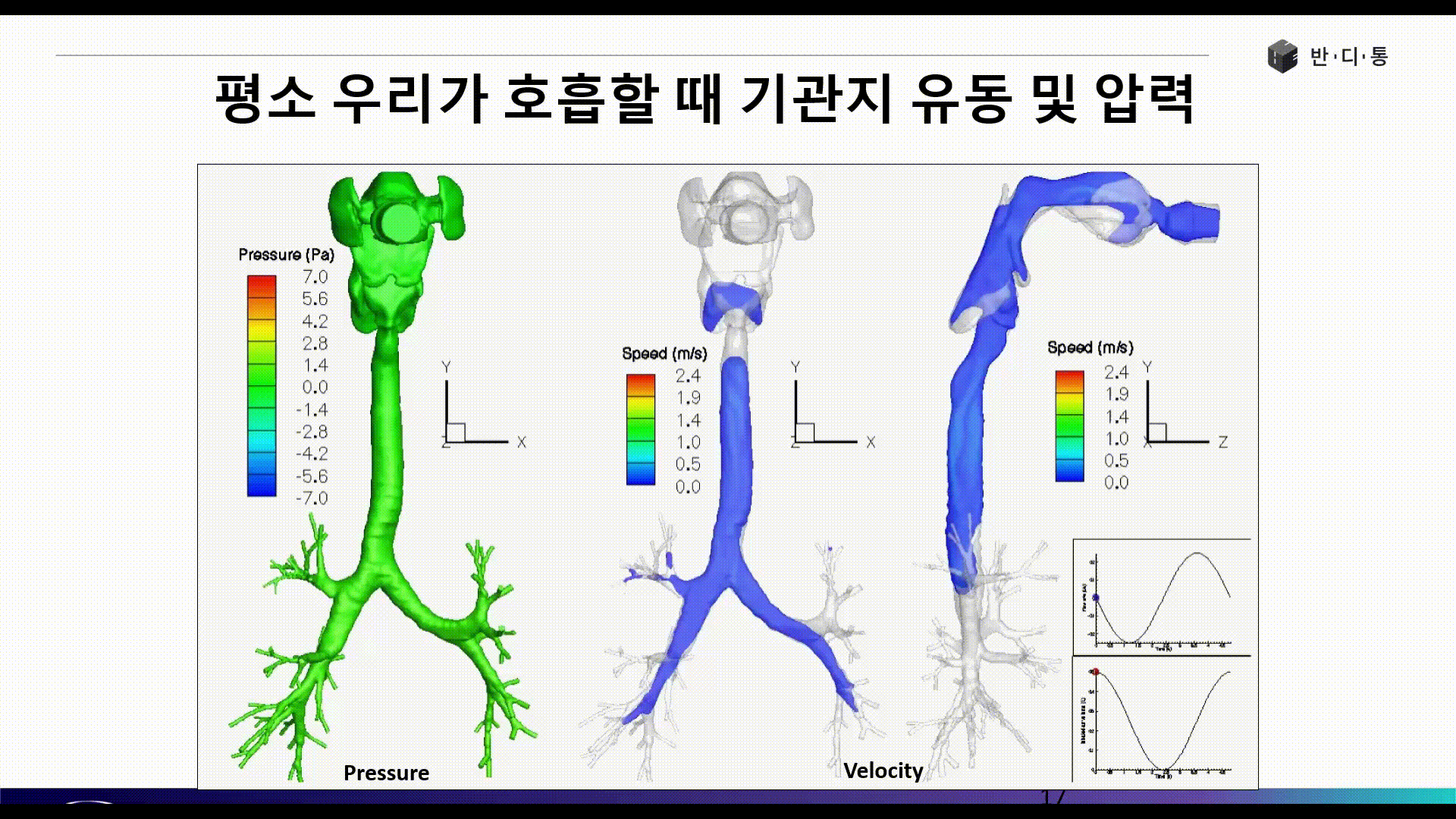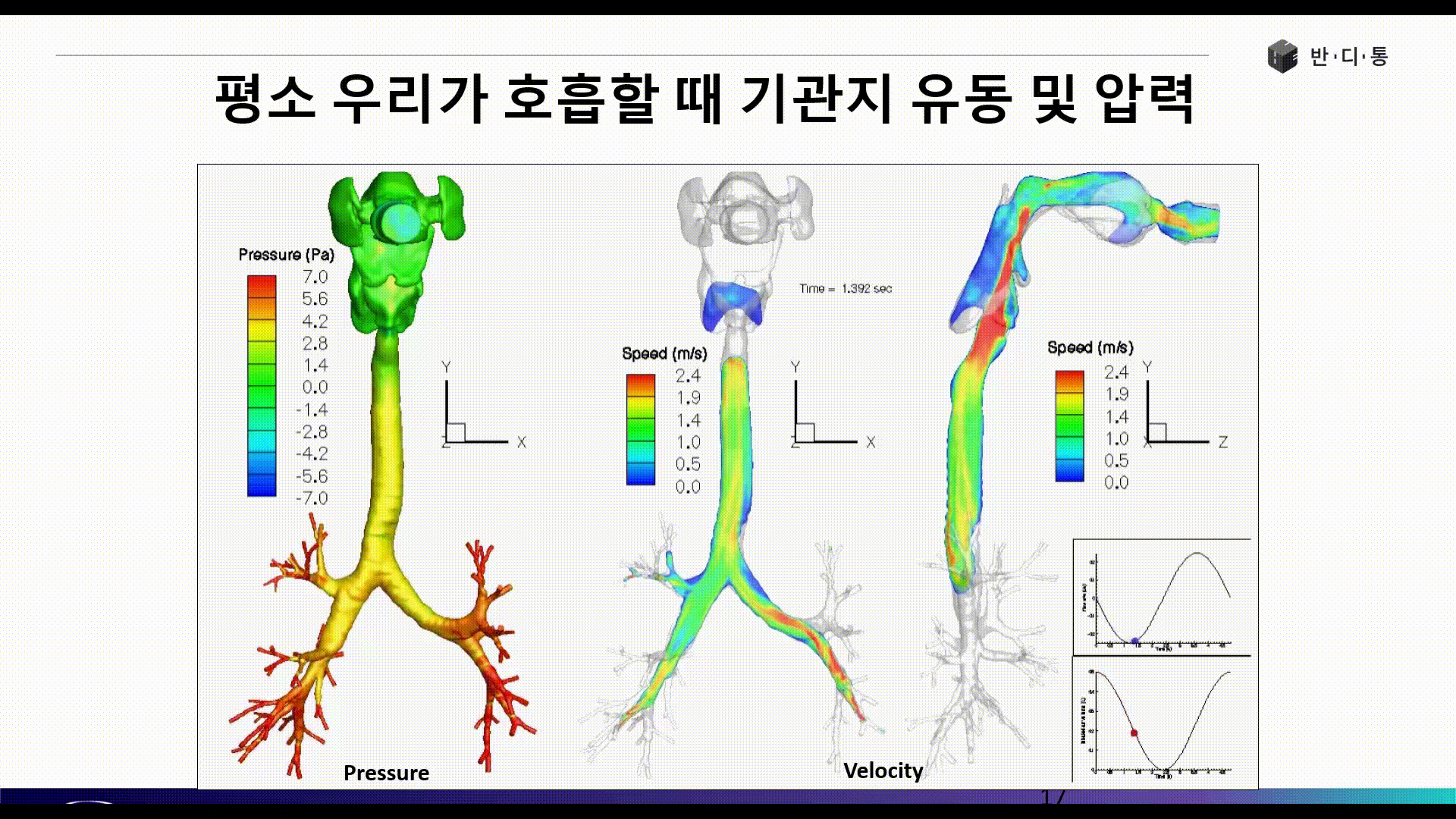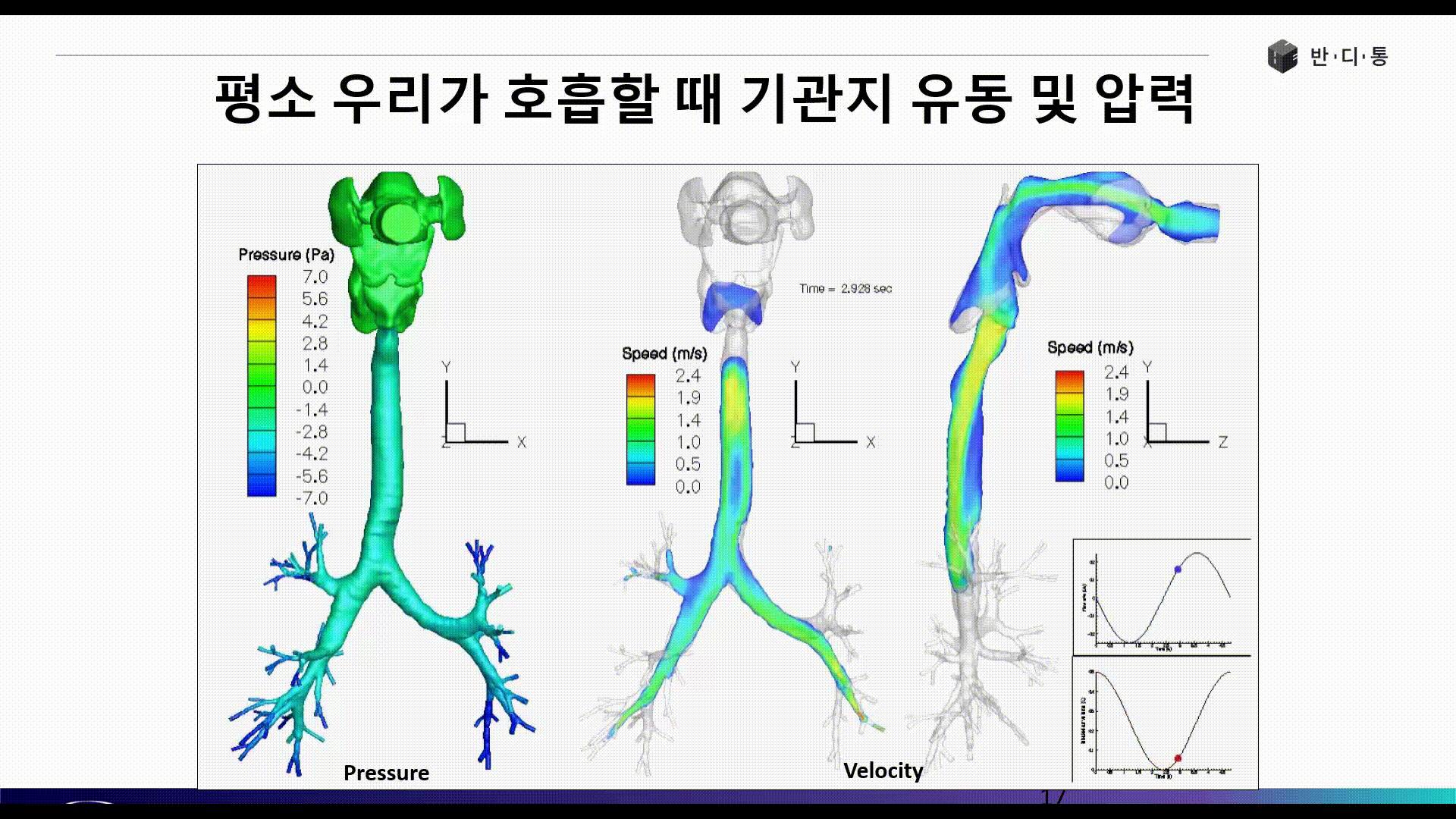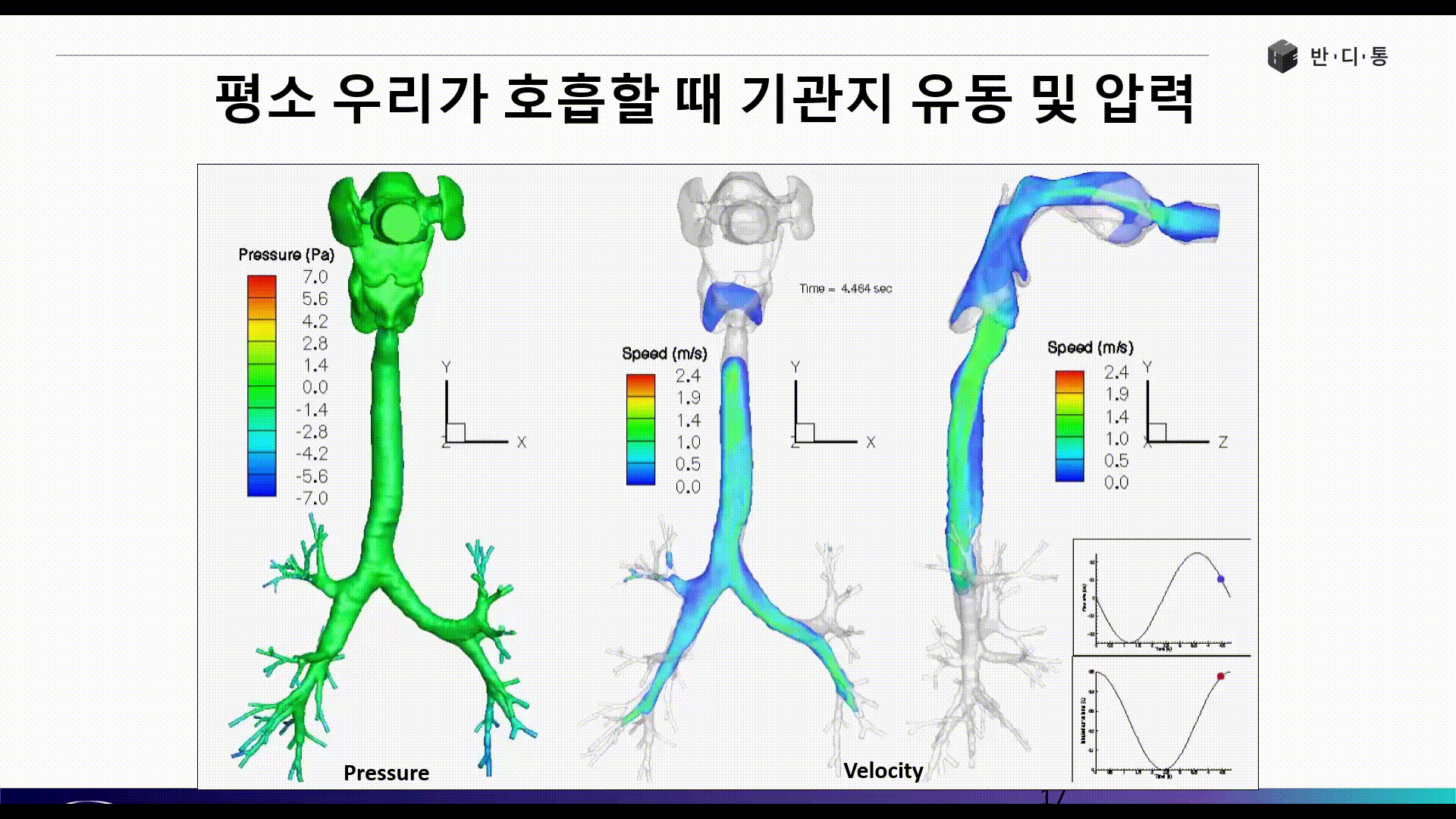
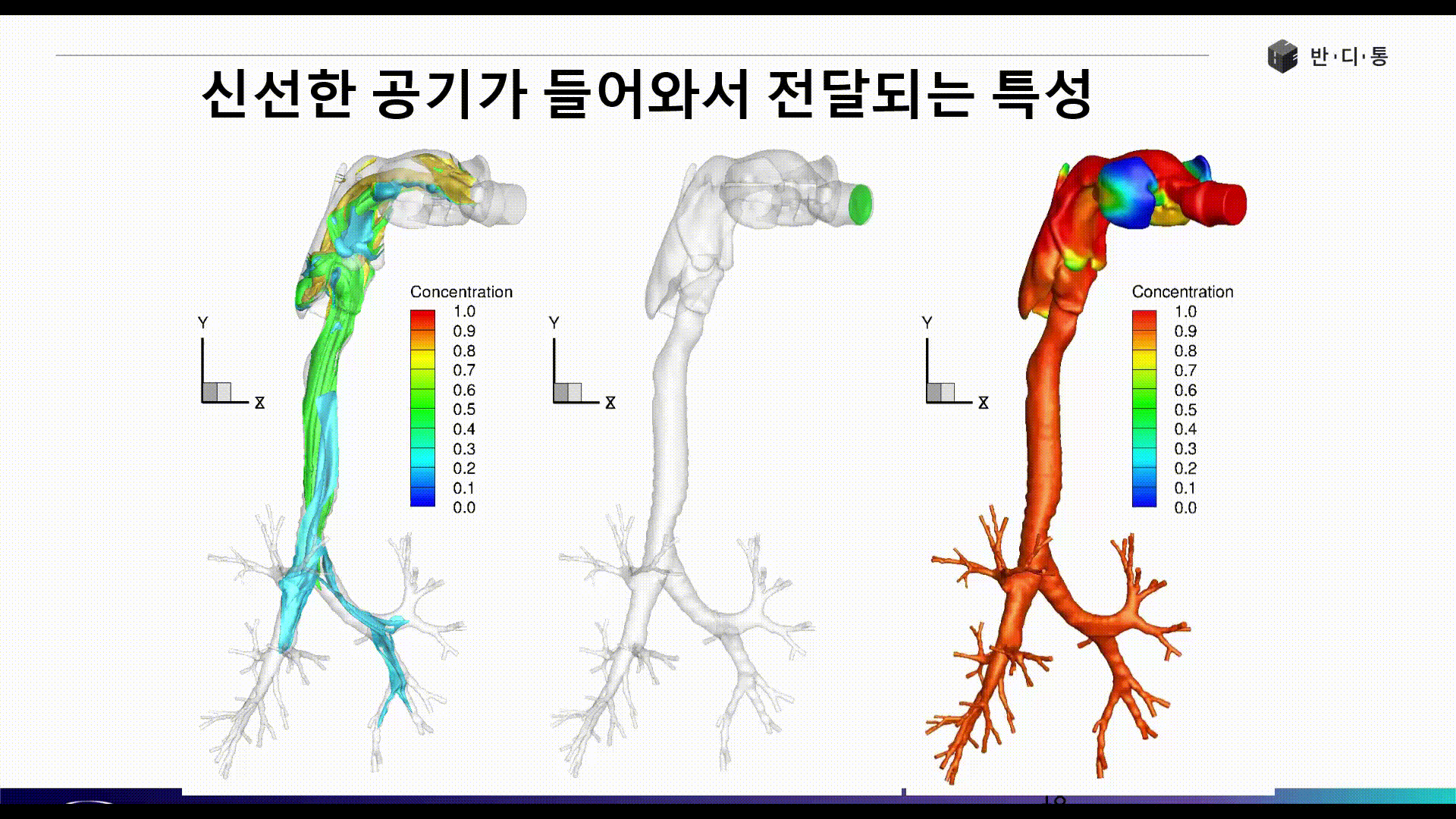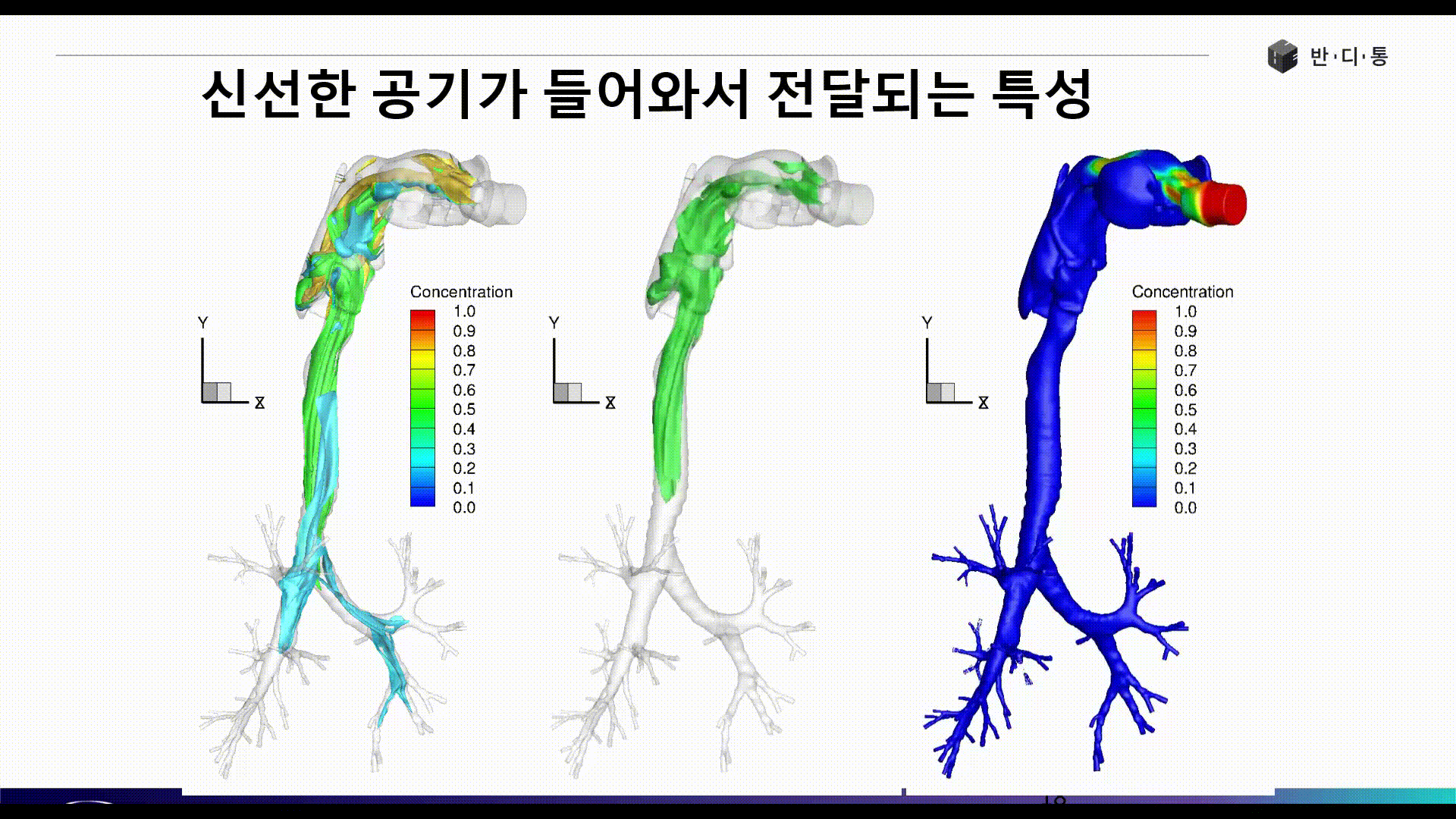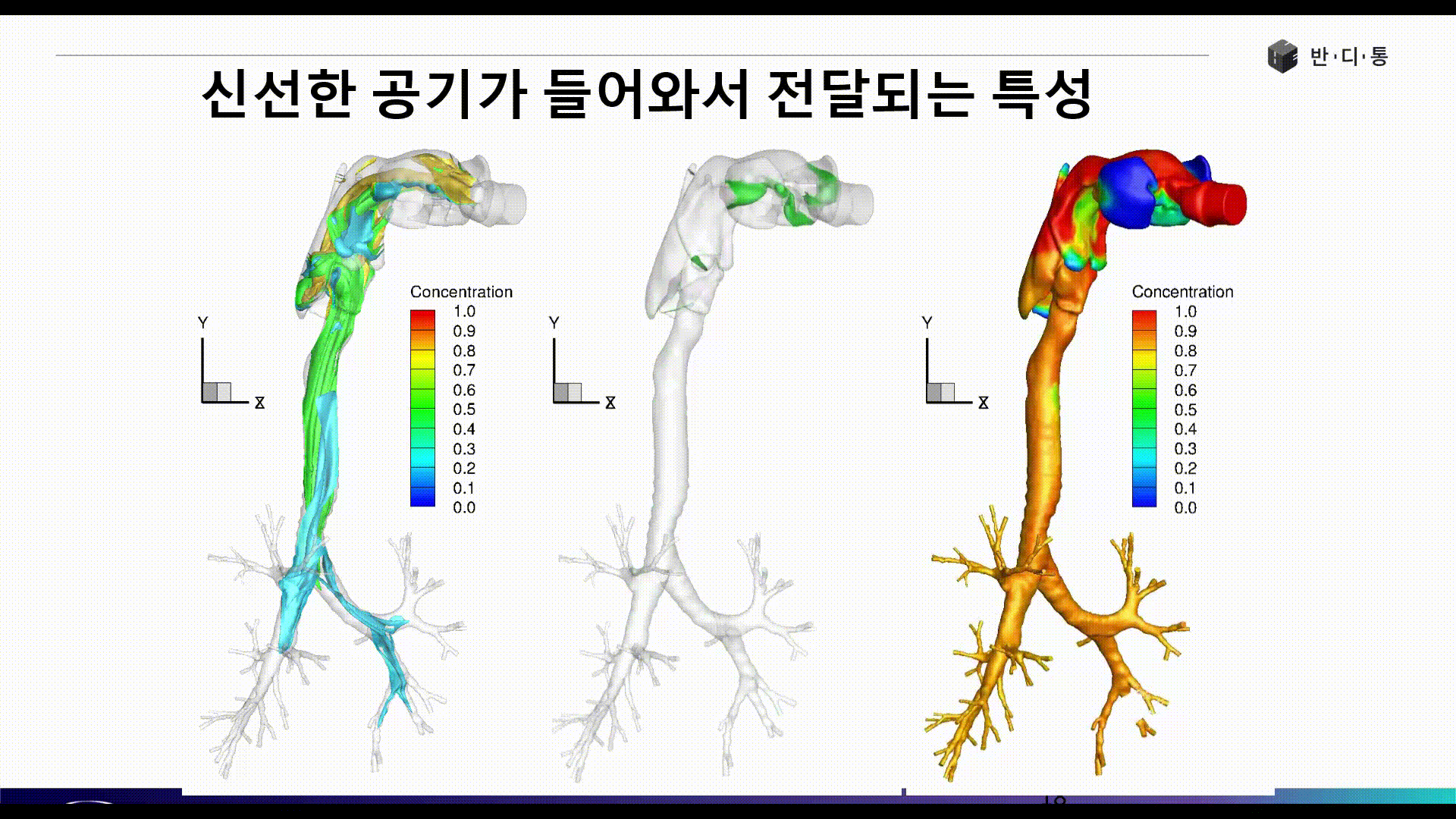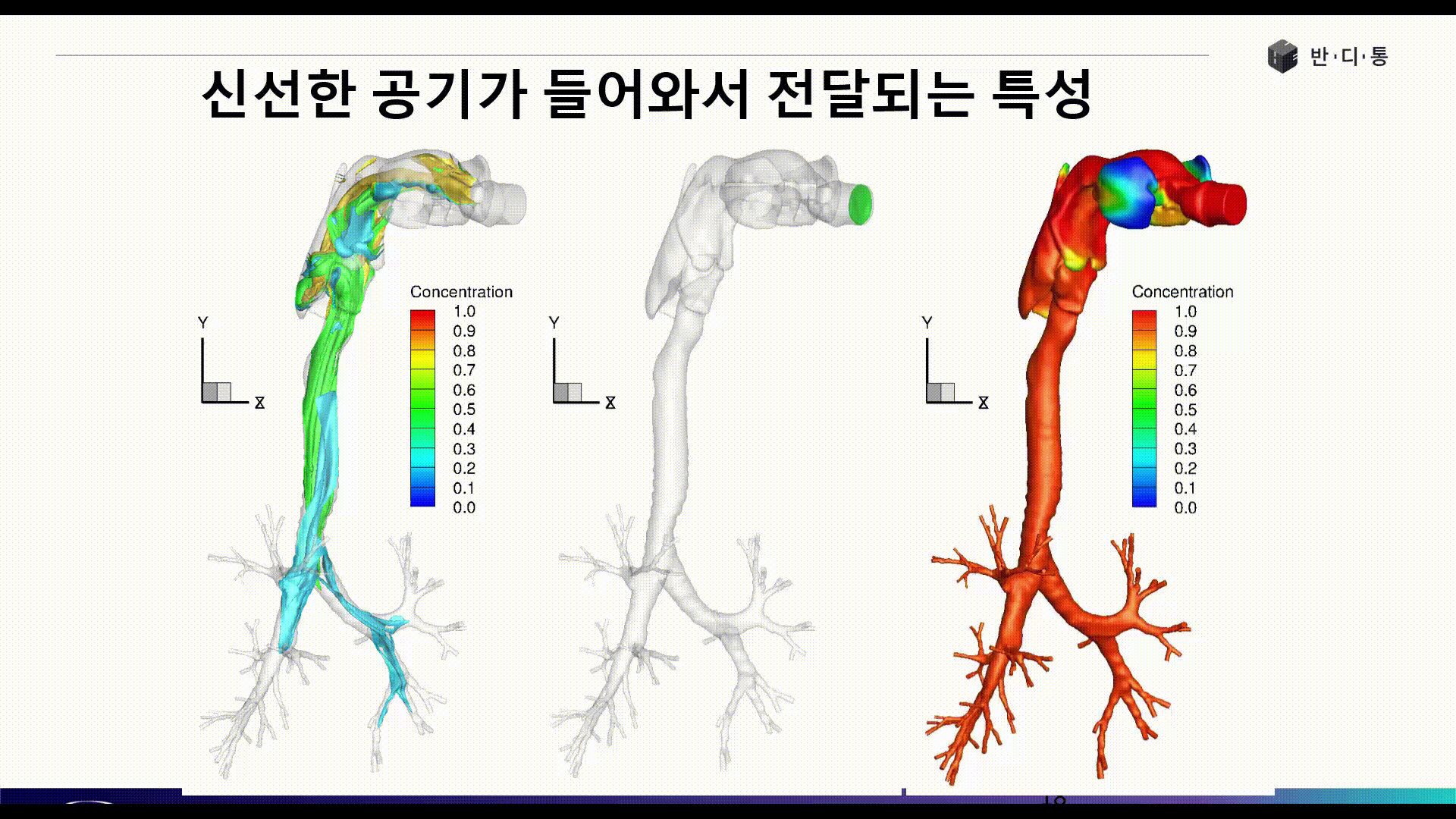
Part 3에서는 폐 해석 사례를 통해 CFD 해석을 위한 요소망 생성(Meshing), 경계조건(Boundary condition) 정의 등 전처리 과정(Pre Process)에 대해 소개합니다.
Part 4. 2상 유동 해석
2상 유동 해석은 액체와 기체와 같이 상(Phase)이 서로 다른 두 물질의 거동을 확인할 수 있는 해석 종류입니다. 액화 물질 이송 차량의 탱크 속 액체의 거동, 자유 수면의 움직임 등을 파악할 수 있는 해석 종류입니다. 2상 유동 해석의 해를 얻기 위한 방정식에 대해 소개합니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
















