임의 물체가 공간 상에서 차지하는 면적 혹은 체적을 수학적으로 계산하는 것을 통칭하여 적분(integration)한다고 말하듯이, 시간에 따라 변하는 물체의 거동을 시간을 따라 추적(track)해 나가는 것을 시간적인 측면에서의 적분이라고 부른다. 예를 들어 지진파를 받는 고층건물 내 임의 한 지점의 시간에 따른 동적인 변형을, 수치해석(numerical analysis)으로 추적하여 시간을 수평축으로 하고 변형량을 수직축으로 하는 함수로 나타낸 것은 시간적분의 결과이다.
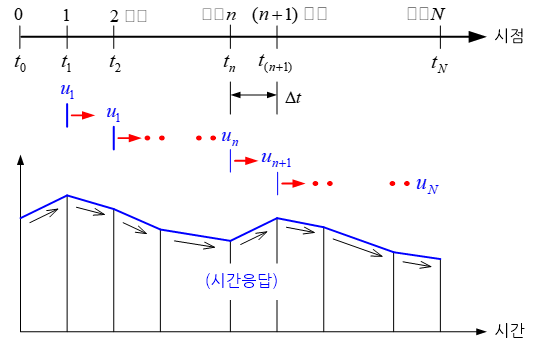
지진파와 같은 동적 외란을 받는 임의 물체의 거동은 뉴튼의 법칙(Newton’s law) 중에서 제 2법칙인 운동의 법칙으로 표현된다. 다시 말해, 외력을 받아 운동하는 물체의 가속도는 외력의 크기에 비례한다. 이 운동법칙에 대한 수학적 표현 속에는 물체 거동의 시간에 대한 변화율과 이 변화율의 시간 변화율이 포함되어 있다. 운동 중인 물체의 위치(혹은 변형)가 관심이 되는 경우, 전자는 속도 그리고 후자는 가속도가 된다. 이러한 시간에 따른 물체의 거동, 즉 초기치 문제(initial value problem)를 유한요소법(finite element method)으로 풀기 위해서는 대상이 되는 전체 시간 구간을 특정한 시간 간격(time step)으로 유한 개의 시점으로 나누어야 한다. 그리고 각 시점에서의 물체의 거동을 구하여 이 값들을 연결하여 연속적인 시간 함수로 표현하면 된다.
각 시점에서 물체의 거동은 초기값(initial value)을 운동방정식에 대입하여 다음 시점에서의 거동을 계산하고, 다시 이 계산된 값을 대입하여 그 다음 시점에서의 값을 구하는 반복계산으로 구해진다. 이러한 반복계산을 통해 원하는 시점까지 물체의 거동을 수치적으로 구하는 개념이 시간적 측면의 적분에 해당된다. 이러한 시간적분에는 크게 암시적 시간적분(implicit time integration)과 명시적 시간적분(explicit time integration) 두 종류가 있다.
.