스프링에 힘을 가해 잡아당기면 길이 방향으로 늘어나게 되는데, 늘어나는 길이는 가해진 힘의 크기와 스프링 상수(spring constant)에 의해 결정된다. 만일 늘어난 길이가 힘에 비례하고 스프링 상수에 반비례 관계에 있다면 이 스프링은 선형(linear)적인 거동을 나타낸다고 할 수 있다. 하지만 힘의 크기에 비례하지 않고 스프링 상수에 반비례적인 관계에 있지 않다면 스프링은 비선형(nonlinear)적 거동을 나타낸다고 말할 수 있다.
이러한 개념은 유한한 체적을 가진 일반적인 탄성체(elastic body)에도 그대로 적용된다. 선형해석(linear analysis)에서는 물체의 변형(deformation)은 외부 하중에 대해 선형적인 관계를 나타내기 때문에, 강성행렬(stiffness)은 일정한 값을 유지한다. 하지만, 물체의 변형이 외부 하중에 대해 비선형적인 거동을 나타내는 비선형 해석(nonlinear analysis)에 있어서 강성행렬은 일정한 값이 아니라 물체 거동의 크기에 따라 계속해서 변한다. 따라서 비선형 해석에 있어서는 이렇게 물체 거동에 따라 변하는 물체의 강성행렬을 계속적으로 갱신해야 하는 번잡한 계산과정이 필요하다.
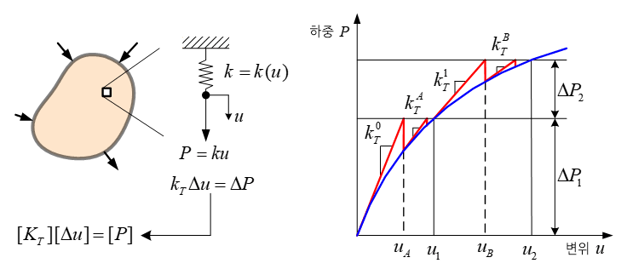
물체의 거동에 따라 변하는 물체의 강성을 정의하는 하나의 방법으로 접선계수(tangent stiffness)라는 것이 있다. 이것은 용어 그 자체가 의미하듯이 물체의 거동값에 해당하는 물체의 강성을 물체 거동 곡선의 접선으로 정의하는 방법이다. 유한요소 해석(finite element analysis)에 있어서 이러한 접선은 행렬 방정식으로 전환하였을 때, 하나의 행렬로 표현되며 이 행렬을 접선계수 행렬이라고 부른다.
그리고 이 접선계수 행렬은 비선형 해석을 위해 주로 사용되는 뉴튼-랩슨 기법(Newton-Raphson method)과 같은 반복계산 기법에 있어 물체 거동의 증분(increment)을 계산하기 위해 사용된다.
.