
설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
통합검색


Search Close

설계 시간이 길어지고 있나요? 효율적인 해석으로 시간을 절약해보세요!
[맞춤 솔루션 알아보기]
유한요소 해석(finite element analysis)을 위해 물체의 기하학적 영역을 유한 개의 작은 영역들로 나누는 요소망 생성 작업(즉, meshing 작업)은 크게 프로그램이 자동으로 처리하는 방식과 해석자가 직접 처리하는 방식으로 나뉜다. 전자에 의해 생성된 요소망을 자동 요소망(auto mesh) 그리고 후자에 의해 생성된 요소망을 수동 요소망(manual mesh)이라고 부른다.
자동 요소망은 해석자가 요소망 생성을 위해 필요한 기본적인 사항만 입력하면 되는 반면, 수동 요소망은 해석자가 요소 분할 개수, 분할 간격 등의 모든 사항들을 일일이 입력해야 한다. 수동 요소망의 장점은 형상종횡비(aspect ratio)가 크거나 과도하게 찌그러진 요소(distorted element)를 방지할 수 있어 보다 정확한 해석결과를 얻을 수 있다는 점이다. 그리고 물체가 특이성(singularity)을 나타내는 국부적인 영역에 크기가 보다 작은 요소를 가지는 편향 요소망(gradient mesh)을 쉽게 생성할 수도 있는 장점을 지니고 있다.
하지만 수동 요소망은 형상이 간단한 경우에만 적용이 가능하기 때문에 매우 제한적인 단점을 지니고 있다. 한편, 하나의 물체에 대한 요소망을 생성하기 위해서 자동 요소망과 수동 요소망을 혼합 적용할 수도 있다. 이 경우, 특별히 신경을 써야 하는 국부영역에는 수동 요소망을 적용하고 나머지 부분에는 자동 요소망을 적용하는 것이 효과적이다.
.
얇은 박판 구조물(thin-walled structure)에 굽힘을 가하면 구조물내 응력이 경계(boundary) 근처에서 급격하게 증가하는 특이성(singularity)이 발생한다. 이러한 현상을 경계층 효과라고 불리며 구조물에만 한정되지 않고 유체 유동에서도 볼 수 있다. 즉 항공기 날개 주위의 공기 흐름에 있어 공기의 점성(viscosity)에 의하여 날개면에서 공기의 상대적인 속도는 0이 된다. 그리고 항공기 표면에서 매우 짧은 거리에 있는 공기속도는 급속히 증가하는 거동을 나타낸다.
이러한 경계층 효과를 수치해석(numerical analysis)적으로 모사하기 위해서는 많은 주의를 기울여야 한다. 박판 구조물이나 유동에 있어 경계층 효과는 경계면에 수직한 방향으로 거동의 급격한 변화이기 때문에, 경계에 폭이 가장 작은 요소를 배치시키고 경계에서 수직방향으로 편향 요소망(gradient mesh)을 적용하여야 한다. 이 요소망에 있어서 경계에 배치한 가장 작은 요소를 특별히 경계요소(boundary element)라고 부르며, 경계에 수직한 방향으로의 폭은 구조물의 두께보다는 작아야 할뿐더러, 그 크기가 작을수록 효과적이다. 한편 경계에 접선방향으로는 편향된 요소망을 적용할 필요가 없다. 왜냐하면 경계에 접선인 방향으로는 거동의 특이성이 발생하지 않기 때문이다.
.
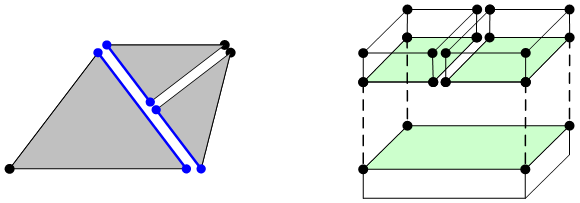
유한요소해석(finite element analysis)을 위해 물체의 형상을 유한 개의 세분 영역들로 나누어 놓은 요소망(mesh) 내 각각의 요소들은 인접한 요소들과 맞붙어 있다. 1차원 선 요소(line element)의 경우에는 좌우 끝 점들은 인접한 좌우 요소들의 끝 점과 정확하게 공유된다. 2차원 삼각형 혹은 사각형 요소는 인접한 요소들과 요소의 변(edge)을 공유하게 되고, 3차원 요소의 경우에는 인접한 요소들과 요소 면(surface)을 공유하게 된다. 만약 한 요소가 하나의 끝 점, 하나의 변 혹은 하나의 면을 통해 오직 하나의 이웃 요소와 접하게 된다면, 이러한 요소망을 정규 요소망(regular mesh)이라고 부른다. 현재 시판되고 있는 대부분의 유한요소 해석 프로그램은 정규 요소망을 사용하고 있다.
하지만, 그렇지 않고 한 요소가 자신의 한 끝 점, 한 변 혹은 한 면에서 하나 이상의 이웃 요소들과 접하게 된다면 이 요소망을 비정규 요소망이라고 부른다. 비정규 요소망은 작은 요소 수로도 높은 해석 정확도를 제공할 수 있는 장점을 지니고 있기 때문에 국부적인 요소망 세밀화(mesh refinement)를 위해 매우 유용하다. 그리고 최근에 소개되고 있는 적응적 hp-유한요소법(adaptive hp-FEM)에서는 이러한 비정규 요소망을 채용하고 있다.
예를 들어, 해의 특이성(singularity)이 존재하는 특정 지점에만 요소망이 매우 조밀하도록 편향 요소망(gradient mesh)을 생성하고자 할 경우, 비정규 요소망은 요소망의 편향(gradient)을 급진전 시킬 수 있기 때문에 최소의 요소 수로 특이점에만 요소망을 매우 조밀하게 조절할 수 있다. 일반적으로 비정규 요소망에서는 1:2의 비율로 하나의 요소가 두 개의 이웃 요소들과 접하도록 하고 있는데, 그 이유는 이 비율이 해석의 안정성과 신뢰성 측면에서 최적이기 때문이다.
.
유한요소 해석(finite element analysis)에 있어 물체의 형상은 물체의 거동에 지대한 영향을 미친다. 특히 구멍이 물체 내부에 존재하거나 꺾어지는 부분 등이 존재하면 이러한 영역에서 물체는 특이(singular)한 거동을 나타낸다. 예를 들어, 동력을 전달하는 기어 축에 기어를 조립하기 위하여 핀(pin) 구멍을 형성하였을 경우, 이 핀 구멍 근처에는 응력집중(stress concentration) 현상이 발생한다. 또한 물체가 예리하게 꺾어져 있는 코너(corner)부나 균열(crack)과 같이 예리한 틈이 존재하는 영역 등에서도 주위와 비교하여 엄청나게 큰 응력(stress)값을 나타낸다.
이렇게 물체의 거동에 특이성을 유발하는 물체의 특수한 형상을 특징 형상이라고 부르고, 유한요소 해석에 있어 해석 결과의 정확성을 확보하기 위해 주의를 기울여야 한다. 보편적으로 특징 형상을 가진 물체영역에는 매우 작은 요소 크기(element size)로 요소망(mesh)을 생성하여야 한다. 그리고 특징 형상 부위로 갈수록 조밀한 요소망이 되도록 편향 요소망(gradient mesh)을 적용하는 것이 해석 결과의 정확성과 해석 시간의 효율성 측면에서 대단히 효과적이다.
.
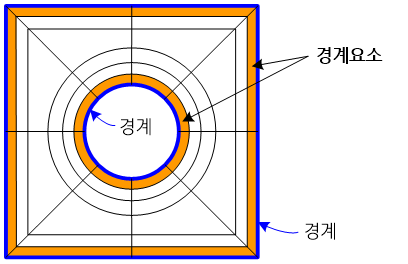
물체의 외곽 가장자리를 그 물체의 경계(boundary)라고 부른다. 예를 들어 1차원 직선의 경우에는 직선의 양 끝점이 경계가 되고 2차원 정사각형의 경우에는 4개의 변이 경계에 해당된다. 한편 3차원 구(sphere)는 구의 최 외곽 표면이 경계에 해당된다. 굽힘변형이 지배적인 박판 구조물(thin-walled structure)에서는 이 경계에서 거동의 특이성(singularity)이 발생하여, 경계부근에서 응력(stress)이 매우 큰 값으로 급격히 증가한다. 그 결과, 주의를 기울이지 않고 요소망(mesh)을 생성하여 유한요소 해석(finite element analysis)을 수행하게 되면 엉터리 결과를 구하게 되는 경우가 허다하다. 이렇게 물체의 경계 부근에서 발생하는 거동의 특이성을 경계층 효과(boundary effect)라고 부른다.
이러한 경계층 효과를 효과적으로 그리고 정확하게 모사하기 위해서는 물체의 경계에서 법선방향으로 폭이 매우 좁은 유한요소(finite element)를 사용하면 되는데, 이 유한요소를 특별히 경계요소라고 부른다. 경계요소의 특징은 경계에서 수직한 방향으로는 그 폭이 물체 두께보다 현저히 작은 반면, 경계에 접선 방향으로는 크기가 작아야 할 필요는 없다. 다시 말해, 경계에 수직한 내면방향으로 편향 요소망(gradient mesh)을 생성하면 효과적이다.
.
해석 정확도를 높이고, 반복 작업을 줄여보세요.
내게 맞는 솔루션 찾기