TAGS : 편차응력

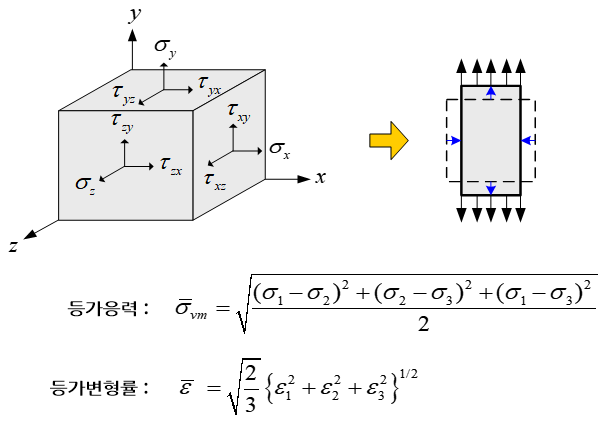
외부로부터 하중을 받고 있는 임의 물체에 있어 그 내부에 발생하는 저항력인 응력(stress)은 방향별 성분을 지니고 있다. 따라서 물체내 임의 지점에서 응력의 절대적인 크기는 임의 응력 성분 하나만으로는 결정할 수 없다. 폰 미제스 응력(von Mises stress)으로 불리는 등가응력(equivalent stress)은 임의 지점에서의 응력의 절대적인 크기를 나타내기 위해 가장 많이 사용되고 있다.

응력과 마찬가지로 물체 변형의 크기를 나타내는 변형률(strain)도 방향별 성분을 지니고 있기 때문에 어느 한 성분만으로 변형률의 절대적인 크기를 나타낼 수 없다. 따라서 물체 내 임의 지점에서 변형률의 절대적인 크기를 나타내기 위한 척도가 필요하다. 등가 변형률은 이러한 변형률의 절대적인 크기를 나타내는 척도로 사용되고 있고 있으며, 물리적으로 등가응력과 짝을 이루는 물리량으로 생각할 수 있다.

보다 정확한 표현으로 등가 변형률은 편차응력(deviatoric stress)과 역학적으로 관계를 맺는다. 등가 변형률은 변형률 성분 각각의 제곱을 모두 합한 값에 2/3를 곱하여 제곱근을 취하여 계산되며, 금속성형(metal forming)과 같은 소성변형(plastic deformation) 거동을 표현하는 소성모델(plastic model)의 변수로 사용되고 있다.

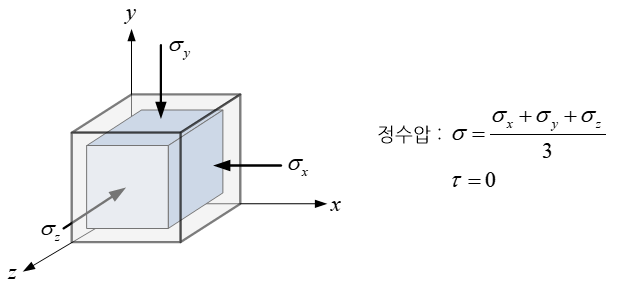
바닷물 속에 잠겨 있는 물체는 물의 수압에 해당하는 압력을 물체 전 표면을 통해 균등하게 받게 된다.  그리고 압력은 물체의 표면에 수직하게 작용하기 때문에 물체 내부에는 수직응력(normal stress)만 발생하고 전단응력(shear stress)은 전혀 발생하지 않는다. 그 결과 찌그러짐과 같은 물체의 형상 변화는 전혀 발생하지 않고 물체 전체의 부피(체적)만 감소한다.

이와 같은 물리적 특성은 외부 하중에 의해 물체 내부에 발생하는 응력(stress)에도 적용할 수 있다. 즉, 물체 내부의 응력은 물체의 체적만을 변화시키는 성분과 형상만을 변화시키는 성분으로 나눌 수 있다. 전자를 정수압에 해당하는 성분이라고 한다.

3차원적인 응력 상태를 나타내는 경우, 3개의 직교하는 축 방향으로의 수직응력들의 총 합을 3으로 나눈 평균값을 정수압으로 정의하고 있다. 그리고 이 정수압을 뺀 나머지 응력 성분들(공학적으로 편차응력(deviatoric stress)이라고 부름)은 물체의 찌그러짐과 같은 모양의 변화를 야기한다.

한편, 정수압은 물체의 체적 변화만을 야기시키기 때문에 소성변형(plastic deformation)에는 아무런 영향을 미치지 않는다. 다시 말해, 물체의 영구적인 변형은 물체의 찌그러짐과 같은 물체의 형상 변화 때문에 발생하는 것으로, 정수압 성분을 뺀 나머지 응력 성분에 의하여 발생하는 것이다. 정수압과 물체의 체적 변화는 체적 탄성계수(bulk modulus)를 통해 상관관계를 맺게 되고, 체적 탄성계수가 커질수록 정수압에 대한 물체의 저항력은 커져서 체적 변화는 감소한다.

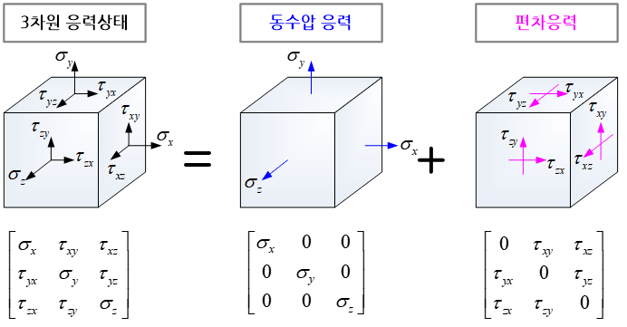
응력(stress)은 외부 하중에 대한 물체의 내부 저항력으로써 물체 단위 면적당 저항력으로 정의된다. 그리고 하중이 크기뿐만 아니라 방향을 가지고 있기 때문에 응력 역시 방향별로 성분을 지니고 있다. 물체의 임의 한 단면에 한정하면 응력은 면에 수직인 수직응력(normal stress)과 면에 평행한 전단응력(shear stress)으로 구성된다. 3차원 물체 내 임의 한 지점을 미소 체적의 육면체로 생각할 경우, 각 면에 하나의 수직응력과 두 개의 전단응력을 지니고 있다.

이와 같은 3차원 물체 내 응력성분들은 크게 정수압(hydrostatic pressure)과 편차응력의 합으로 표현된다. 전자는 물체의 형상은 변화시키지 않으면서 물체의 체적을 증감시키는 역할을 한다. 예를 들어, 물 속에 잠겨있는 물체는 수압을 받게 되고 그 결과 물체의 전체 체적이 감소한다. 이 경우, 물체의 형상은 변화지 않기 때문에 물체 내부에는 동수압에 해당하는 응력 성분들만 존재하고, 전단응력에 해당하는 편차응력은 전혀 발생하지 않는다. 그리고 물체 내부에 발생하는 세 방향으로의 수직응력을 합하여 3으로 나누면 정확히 수압과 일치한다. 이러한 맥락에서 응력 성분들 중에서 세 방향으로의 수직응력을 합하여 3으로 나눈 값을 동수압이라고 부른다.

 편차응력은 물체 내 임의 지점에서의 응력 성분들에 동수압 성분을 뺀 나머지로 정의된다. 편차응력은 물체의 체적 변화에는 영향을 미치지 않고 물체를 형상을 찌그러지게 하는 역할을 하며, 그 결과 소성변형(plastic deformation)을 야기한다. 편차응력은 소성변형 해석에 사용되며, 세 개의 불변량을 가지고 있는 데, 각각 J₁, J₂ 그리고 J₃로 불린다. 이들은 물체 내 임의 지점에서 좌표축의 방향과는 무관하게 항상 일정한 값을 지니며, 항복여부를 판단하는 항복조건(yield criterion)의 매개변수로 사용된다.