통합검색


Search Close


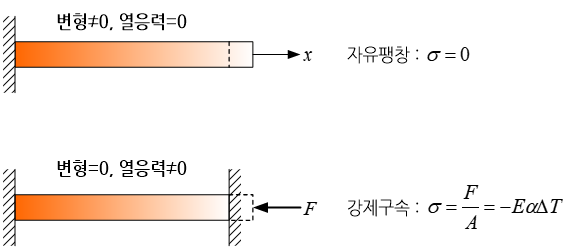
물체는 열을 받으면 그 체적이 증가하는 반면 냉각이 되면 반대로 체적이 감소한다. 하지만 물체를 늘어나거나 줄어들지 않도록 구속하게 되면 물체 내부에는 이 구속에 저항하려는 내력이 발생하게 된다. 예를 들어 가느다란 원형 단면의 금속 봉을 아무런 구속없이 열을 가하면 자유로이 늘어난다.
하지만 이 금속 봉을 길이방향으로 늘어나지 못하도록 양 끝을 구속한 상태에서 열을 가한다고 생각해 보자. 그러면 금속 봉은 구속하고 있는 물체에 힘을 가하는 반면 구속하고 있는 물체는 금속 봉에 크기가 같고 방향이 반대인 반력을 가하게 된다. 그 결과 금속 봉은 외부로부터 힘을 받는 상태와 같게 되고 이로 인해 내부에 저항하려는 내력이 발생하게 된다.
그리고 금속 봉의 단위 면적당의 저항력을 열응력이라고 부른다. 열응력의 크기는 열을 받는 물체의 고유한 재료 물성치인 열팽창계수(thermal expansion coefficient)와 온도 증가에 비례한다. 물체가 아무런 구속없이 자유로이 팽창 혹은 수축하는 경우에는 열응력은 발생하지 않는다. 하지만 물체가 구속이 되어있지 않다고 하더라도 물체 전 영역에서 온도분포가 일정하지 않기 때문에 이러한 온도구배로 인하여 내부에 열응력이 발생하게 된다. 가장 대표적인 예로 용접 후 물체 내부에 남게되는 잔류 열응력(residual thermal stress)을 들 수 있다. > 열응력 더 자세히 보기🔎
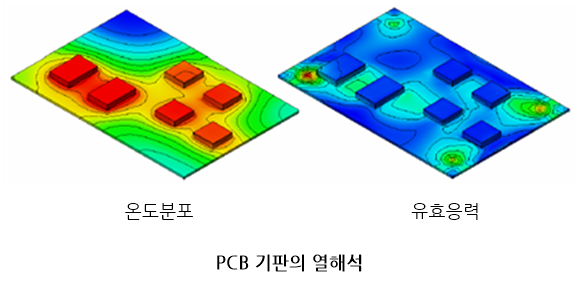
물체가 가열되거나 냉각되면 온도가 변할뿐더러 체적 및 형상도 동시에 변한다. 또한 주변 물체와의 접촉(구속) 상태에 따라 물체 내부에 열응력(thermal stress)이 발생하곤 한다. 열은 크게 세가지 경로를 통하여 전달되는데, 하나는 금속과 같은 고체(solid)를 통하여 전달되는 전도(heat conduction), 공기나 물과 같이 기체 및 유체를 통해 전달되는 대류 열전달(heat convection), 그리고 나머지 하나는 진공상태를 통한 복사 열전달(heat radiation)이다.
이와 같은 열전달에 따른 물체의 온도변화, 그리고 온도변화에 따른 물체의 열변형 그리고 열응력을 수치해석(numerical analysis)적으로 계산하는 작업을 통상적으로 열해석이라고 부른다. 열해석은 위에 언급한 거동들이 시간에 따라 변하는 경우를 다루는 비정상상태(unsteady state) 열해석과 시간에 따른 변동이 없는 정상상태(steady state) 열해석으로 대별된다.
또한 위 거동들이 선형(linear)적인 경우를 선형 열해석이라고 부르고, 비선형성(nonlinearity)을 가지는 문제에 대한 해석을 비선형 열해석이라고 부른다. 열해석은 용접이나 금속성형을 필두로 하여 반도체와 같은 전기,전자산업분야에 이르기까지 매우 광범위한 분야에 적용되고 있다. > 열해석 더 자세히 보기🔎
천이라는 용어는 성질이나 특성이 서로 다른 두 개체 사이의 급격한 변화를 완화시키는 것을 의미한다.
예를 들어 고속으로 비행 중인 항공기 날개 주위의 공기흐름과 항공기로부터 멀리 떨어져 있는 곳에서의 공기흐름은 현저하게 다른 특성을 나타낸다. 그리고 이 두 영역 사이에는 두 가지 뚜렷한 공기 흐름이 완만하게 변화하는 천이영역(transition region)이 존재한다. 만약 이러한 천이영역이 존재하지 않는다고 가정하면 서로 뚜렷한 특성을 나타내는 두 공기흐름 사이의 엄청난 속도 차이로 어떠한 현상이 발생할지 예측하기 어렵다.
재질이 서로 다른 두 물질을 단순히 적층시킨 적층 복합재(heat-proof composite)의 경우, 접착면에서 금속 재질의 예리한 물성치 차이로 과도한 열응력(thermal stress) 집중현상이 발생한다. 그 결과 접착면에서 두 물질이 분리되거나 파손이 발생하기 쉽다. 이처럼 두 가지 서로 다른 성질이나 특성을 가지는 개체 사이를 천이시키지 않으면 예상하지 않은 다양한 문제점들이 발생할 것이다.
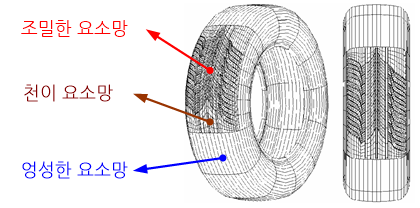
유한요소 해석(finite element analysis)에 있어 요소 유형, 요소 크기(element size), 요소 차수(element order) 등과 같은 특성이 서로 다른 요소망(mesh)을 서로 결합시키고자 할 경우에도 특별한 기법들이 요구되기 때문에 어려움이 많다. 이러한 경우, 서로 다른 두 요소망 사이에 천이 요소망을 적용하면 특별한 기법을 사용하지 않고서도 원활하게 두 요소망을 결합시킬 수 있다.
예를 들어 요소 크기가 서로 다른 두 요소망을 결합시키는 경우, 요소 크기가 점진적으로 변하는 천이 요소망을 두 요소망 사이에 삽입하여 결합시키면 된다. 요소 차수나 유형이 서로 다른 두 요소망을 결합시키는 경우에도 이들 인자들이 한 요소망에서 결합될 또 다른 요소망으로 점진적으로 변화하도록 천이 요소망을 삽입시켜 두 요소망을 결합시키면 된다.
.