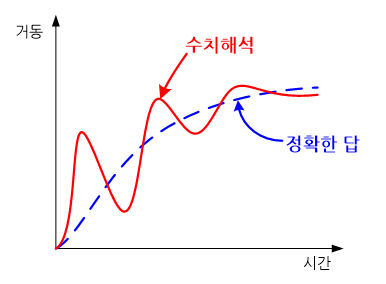
지진파와 같은 외란을 받는 구조물은 시간에 따라 지속적으로 변화는 동적응답을 나타낸다. 그리고 이러한 동적 응답(dynamic response)은 진폭의 변화가 극심하고 불안정한 과도응답(transient response)과 진폭의 변화가 작고 안정적인 정상상태(steady-state)에 가까운 응답으로 구분된다. 시간에 따른 물체 거동의 수치해석은 관심이 되는 시간 구간을 유한 개의 시점으로 나누고, 각 시점에서의 응답을 시간적분(time integration)이라 불리는 수치기법으로 순차적으로 구하게 된다.
그런데 순차적으로 응답을 구할 경우, 시점과 더불어 응답 값의 요동(oscillation)이 줄어들지 않고 계속해서 증가하는 일이 발생하곤 한다. 이처럼 시간적분을 통해 구한 응답이 시점과 더불어 계속해서 요동이 증가하는 것을 해가 불안정하다고 말하고, 반면 요동이 점차적으로 줄어드는 것을 해가 안정적이라고 말한다.
해의 안정성은 해의 수렴성(convergence of solution)과는 뚜렷한 차이가 있다. 전자는 시간적분으로 구한 물체의 거동이 시점과 더불어 그 요동이 줄어듬을 의미하는 반면, 후자는 시점과 더불어 해의 오차(error)가 줄어드는 것을 의미한다. 해의 수렴성과 마찬가지로 해의 안정성도 시간적분을 위해 사용되는 수치기법과 시간 간격(time step) 및 요소 크기(element size)에 절대적으로 좌우된다.
예를 들어, 어떠한 시간적분 기법은 시간 간격과 요소 크기와는 무관하게 항상 안정적인 응답을 제공하는 반면, 다른 기법들은 이들 파라메터가 특정한 조건식을 만족할 경우에만 안정적인 응답을 제공한다. 전자와 같은 시간적분법을 무조건적으로 안정(unconditionally stable)한 수치기법이라 불리는 반면, 후자와 같은 시간적분법을 조건적으로 안정(conditionally stable)한 수치기법으로 불린다.
.