유한요소 해석(finite element analysis)에 있어 해석결과의 정확성은 무엇보다 중시해야 할 사안이다. 유한요소 해석은 근사해를 구하는 수치기법이란 점에서 항상 오차(error)를 수반하고 있으며, 이 오차는 자연현상을 유한요소 해석 모델로 전환하는 과정에서 수반되는 모델링 오차(modeling error)와, 이 유한요소 해석 모델을 수치해석적으로 계산하는 과정에서 수반되는 수치해석 오차(numerical analysis error)로 구성된다. 이 두 가지 오차성분은 모델을 보다 정확하게 구성하고 또한 요소망(mesh)을 세밀화시키면 줄어든다.
이와 같이 유한요소 해석결과에 영향을 미치는 각종 파라메터를 조정하면 오차가 줄어드는 경향을 해의 수렴성이라고 부른다. 대부분의 경우, 이러한 파라메터를 조정하면 오차는 줄어들지만 그렇지 않은 경우도 가끔 발생한다. 이러한 경우를 해가 발산(diverge)한다고 한다.
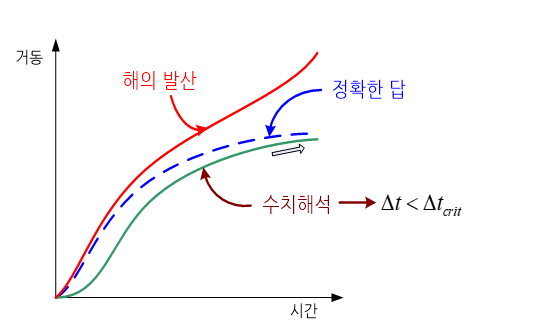
예를 들어 시간에 따른 유체의 거동을 시간적분(time integration) 기법을 적용하여 근사해를 구할 경우, 시간이 경과할수록 수치해가 정확한 답으로부터 멀어지는 경우가 종종 있다. 이러한 수치기법들은 해의 수렴성을 보장하지 않는 기법이라고 부르며, 이러한 경우는 해석결과에 영향을 미치는 각종 파라메터들이 까다로운 조건식들을 만족할 경우에만 해의 수렴성이 보장된다.
이처럼 각종 파라메터가 특정한 조건을 만족시킬 때에만, 해의 수렴성이 보장되는 기법을 조건적 수렴성(conditional convergence)을 나타낸다고 부른다. 유동 해석에 있어 반복계산에 따른 해의 수렴성은 필수요건이기 때문에, 적용하고자 하는 수치기법의 특성을 정확히 파악하고 있어야 한다.