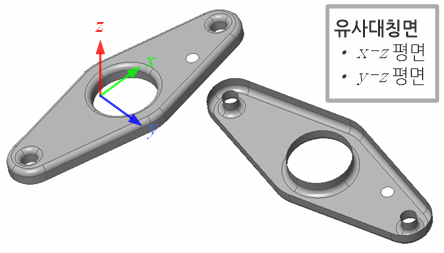
임의 자연현상이나 물체의 거동이 특정한 선, 면 혹은 축을 중심으로 대칭이 되는 경우를 대칭문제(symmetric problem)라고 부른다. 대칭에는 완전 대칭과 유사 대칭으로 구분할 수 있다. 전자는 물체의 형상, 재질, 하중상태 및 구속조건이 완전히 대칭이 되는 경우를 말한다.
하지만, 이러한 완전 대칭 조건을 만족하지는 않지만 거의 유사하게 대칭이 되는 경우를 종종 발견할 수 있다. 예를 들어, 위에서 언급한 대칭 조건의 요구사항들 중에서 일부가 대칭성을 조금 이탈한 경우가 이에 해당된다.
재질, 하중상태 및 구속조건이 완전히 대칭을 이루지만 형상적인 측면에서 한 쪽에는 작은 구멍을 가지고 있는 반면 다른 한 쪽에는 구멍이 없는 경우를 생각해 보자. 이러한 경우, 구멍이 있는 쪽이 구조적으로 취약하다. 따라서 구멍이 없는 쪽에 동일하게 구멍이 있다고 가정하여 대칭문제로 취급하여도 무방하다. 왜냐하면, 원래 형상보다 대칭으로 가정한 형상이 구조적으로 강도가 낮기 때문에 안전율(safety) 측면에서 보다 안전한 설계에 이르게 한다.
이와 같이 우리 주위에는 유사 대칭을 나타내는 문제를 많이 발견할 수 있으며, 완전 대칭으로 가정하여 해석을 효과적으로 수행할 수 있다. 하지만 이렇게 유사 대칭을 완전 대칭으로 가정할 경우, 유념해야 할 사항은 완전 대칭으로 가정한 문제가 원래 문제보다 안전한 설계를 보장할 수 있어야 한다는 점이다.
한편, 대칭성에서 이탈한 정도가 아무리 미미 하더러도 완전 대칭으로 가정하여 풀 수 없는 문제들도 있다. 예를 들어, 완전 대칭성을 깨뜨리는 사항이 물체 거동에 지배적인 인자라고 한다면 완전 대칭으로 가정하여 풀게 되면 전혀 다른 해답에 도달할 수 있기 때문이다.
.