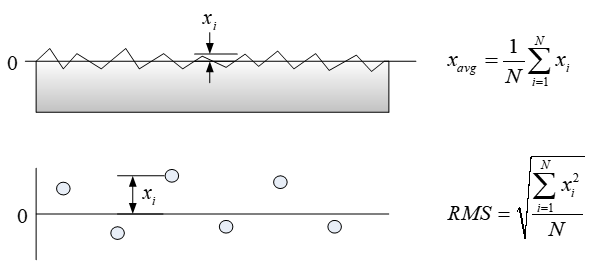
연속적인 분포를 갖는 물리량 혹은 흩어져 있는 데이터의 평균값은 적분치 혹은 총합을 분포의 폭 혹은 데이터의 개수로 나눈 량으로 정의된다. 예를 들어 한 주기를 갖는 사인함수(sine function)의 평균값은 0이 되고, 1부터 10까지 정수들의 평균값은 5가 된다. 이와 같이 평균값은 물리량 혹은 데이터에 있어 양과 음의 값을 구분하여 계산된다.
하지만 때때로 물리량의 양과 음을 구분하지 않고 절대적인 크기에 대한 평균값 개념으로 RMS(root mean square)가 사용되고 있다. 위에서 언급한 한 주기 사인함수의 RMS는 더 이상 0이 아니다. RMS의 정확한 정의는 이 용어가 의미하듯이 물리량을 제곱하여 적분 혹은 합한 다음 분포의 폭 혹은 데이터의 개수로 나눈 값의 제곱근이다.
RMS는 전기나 전자기와 같은 각종 파동(wave)이 지니고 있는 에너지, 물체 표면의 거칠기(roughness) 정도, 각종 오차(error)의 절대적인 크기를 나타내기 위하여 주로 사용된다. 만일 이러한 경우에 일반적인 평균값을 사용한다면 해당 물리량이나 오차 분포의 전체적인 크기를 간과할 수 없다. 유한요소해석(finite element analysis)에 있어서도 RMS 형태로 결과값의 절대적인 평균값을 출력할 수 있다. 주로 동해석(dynamic analysis)이나 수치해석 오차(numerical analysis error) 분석에서 많이 사용된다.
.