거울을 들여다 보면 자신의 모습이 그대로 나타난다. 한가지 뚜렷한 차이는 거울 속에 비추어 지는 모습은 3차원이 아닌 2차원 평면상의 이미지라는 점이다. 이러한 차이를 무시하고 모양 그 자체만 놓고 보면 거울은 자신과 거울 속 이미지 사이의 대칭면(symmetry plane) 역할을 한다. 우리 주위에는 이러한 반사 대칭을 만족하는 물체를 쉽게 발견할 수 있다.
예를 들어, 사각형 액자의 형상은 좌우 혹은 상하로 이등분하여 나누면 나뉘게 되는 한 쌍은 반사대칭을 만족한다. 캔 음료수나 종이컵 역시 전형적인 반사대칭에 해당된다. 물론 이들은 기하학적 형상이 중심 축에 대하여 완전한 축대칭(axisymmetry)을 나타낸다. 이와 동시에 원주방향으로의 임의 각도를 기준으로 180도로 이등분하게 되면 나뉘게 되는 두 쪽은 언제나 반사대칭을 이룬다.
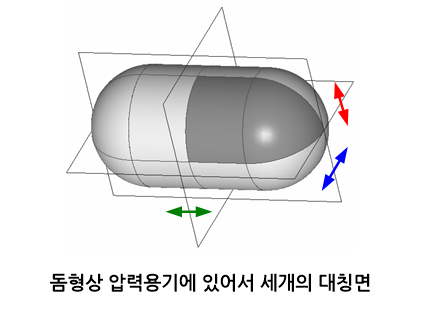
지금까지 말한 대칭성은 기하학적 형상에만 한정한 것으로써, 공학적 의미에서 대칭은 기하학적 형상뿐만 아니라 재질, 구속조건 그리고 하중조건 모두가 대칭성을 만족해야 한다. 따라서 반사대칭 역시 대칭면을 중심으로 나뉘게 되는 두 쪽은 재질, 구속조건 그리고 하중조건이 모두 반사대칭이 되어야 한다. 반사대칭을 이용하게 되면 대상 물체 전체가 아닌 대칭이 되는 어느 한 쪽만 해석하면 되기 때문에 해석시간을 현저히 단축시킬 수 있다. 반사대칭은 해석대상을 2등분에만 국한되지 않고 4등분 심지어 8등분까지 나뉘게 할 수 있다.
.