유한요소법(finite element method)과 같은 수치해석(numerical analysis) 기법은 자연현상의 수학적 표현(대부분 미분방정식 형태)을 행렬방정식(matrix equation)으로 전환하여 컴퓨터를 이용하여 근사적인 해답을 구한다.
행렬방정식을 구성하는 각각의 행렬은 컴퓨터를 이용한 수치적분(numerical analysis)으로 계산하는데, 특히 유한요소법에서 사용되는 수치적분은 일반적인 수치적분과는 달리 오차가 전혀 없는 정확한 수치적분을 적용하고 있다. 그 이유로는 조그마한 수치적분 오차라도 행렬방정식을 푸는 과정에서 누적되어 최종 수치해석 결과에 수용할 수 없을 정도의 큰 수치해석 오차(numerical analysis error)를 유발시키기 때문이다.
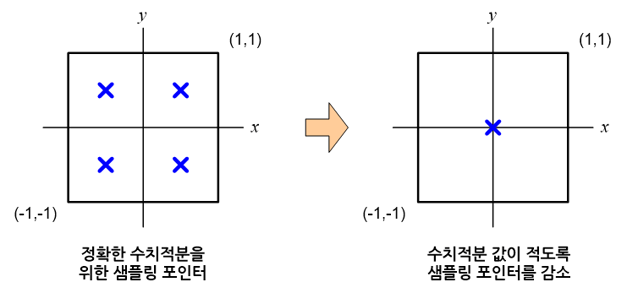
정확한 수치적분을 위해서는 함수의 실제 값을 취하는 샘플링 지점(sampling point)과 그 지점에 대한 가중치(weight)를 수학적으로 유도해야 한다. 정확한 샘플링 지점과 가중치를 계산하는 방법에는 가우스 구적법(Gauss quadrature rule)과 로빠또 구적법(Lobatto quadrature rule)이 있다. 그리고 정확한 수치적분을 위해 사용해야 할 샘플링 지점의 개수와 가중치 값은 적분하고자 하는 함수의 차수에 비례하여 증가한다. 감차적분이란 함수를 수치적으로 정확하게 적분하기 위해 필요한 샘플링 지점의 개수보다 작은 샘플링 지점 개수를 이용하여 수치적분하는 것을 일컫는다. 즉, 정확한 적분값보다 낮은 적분값이 나오도록 의도적으로 계산되도록 하기 위함이다.
.