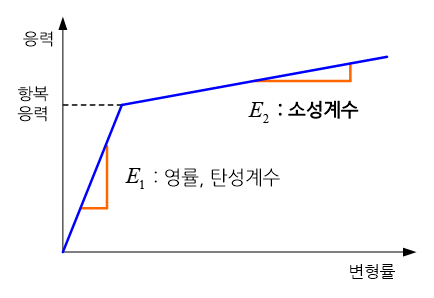
금속과 같은 연성재료(ductile material)는 외부로부터 하중을 받으면, 하중의 크기가 작은 범위에서는 응력과 변형률이 선형적인 관계를 가지는 탄성거동(elastic behavior)을 나타낸다. 그리고 이러한 탄성영역에서 물체의 강성(stiffness)은 변형률 증가에 따른 응력의 기울기, 즉 영률(Young’s modulus)이라 불리는 탄성계수(elastic modulus)로 표현된다. 하지만 하중의 크기가 증가하여 물체 내부의 응력이 항복응력(yield stress)을 초과하게 되면 응력은 더 이상 변형률과 선형적인 관계를 나타내지 않는다.
다시 말해 응력-변형률 선도(stress-strain diagram)가 비선형적인 곡선 형태가 된다. 이러한 소성변형 영역에서 특정 변형률 값에서의 선도의 기울기는 탄소성 접선계수(elastoplastic tangent modulus)로 정의되며, 탄성계수와는 달리 일정한 값이 아니라 변형률에 따라 달라진다. 한편, 소성영역에서 물체의 변형률은 탄성 변형률(elastic strain)과 소성 변형률(plastic strain)의 합으로 표현되는데, 전자는 하중이 제거되면 사라지는 반면 후자는 영구변형으로 계속해서 남게 된다.
만일 소성영역에서 물체 내 응력-변형률 선도를 소성변형률의 함수로 표현할 경우, 이 선도의 기울기를 소성계수라고 부르며 탄소성 접선계수와는 다른 의미를 지니고 있다. 소성계수 역시 탄성계수와는 달리 소성변형률 값에 따라 변하는 값으로 특정 소성 변형률 값에 대한 선도의 기울기로 정의된다.
.