유한요소해석(finite element analysis)을 수행한다는 것은 대상이 되는 해석문제를 표현하는 수학적 표현식을 행렬방정식으로 변환하여 물체의 거동을 근사적으로 구하는 것이다. 그런데 행렬방정식을 풀어서 구한 값들은 일반적으로 요소망(mesh) 내 각 절점(node)에서의 물체의 거동값에 해당된다. 예를 들어 열전달 해석으로 구한 수치값들은 대상이 되는 물체의 요소망 내 각 절점에서의 온도를 나타낸다.
이처럼 요소망 내 각 절점에서의 값들을 절점 값이라고 부르고, 값의 유형에 따라 절점 변위(nodal displacement), 절점 온도(nodal temperature), 절점 하중(nodal force) 등으로 명명된다. 행렬방정식을 풀어서 구한 수치값이 각 절점에서의 값이 되는 것은 물체의 거동을 근사화 하기 위해 사용되는 기저함수(basis function)의 특성 때문이다.
유한요소 해석에 사용되는 대부분의 기저함수는 자신의 번호와 일치하는 절점에서는 1의 값을 가지는 반면 나머지 모든 절점에서는 0의 값을 가지게 된다. 만일 기저함수가 이러한 특성을 지니고 있지 않다면 행렬방정식으로부터 구한 값이 곧바로 절점에서의 거동값을 나타내지 않는다. 이러한 경우에는 거동에 대한 근사식에 해당 절점의 좌표값을 대입하여 그 절점에서의 값을 계산해 내어야 한다.
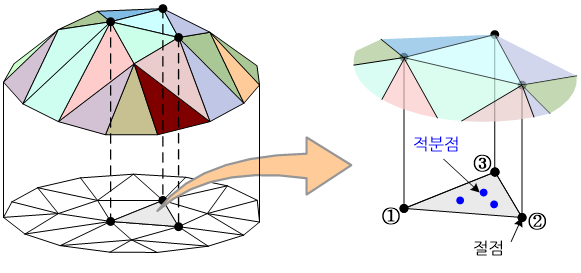
한편, 변형률(strain)이나 응력(stress)은 절점에서 그 값을 계산하지 않고 행렬의 수치적 적분(numerical integration)을 위해 사용되는 적분점(integration point)에서 그 값을 계산한다. 그 이유는 이러한 값들은 절점에서 계산하는 것보다 적분점에서 계산하는 경우가 보다 정확하기 때문이다.
.