Ax=b라는 행렬방정식에서 x라는 해를 계산하는 경우를 생각해 보자. 만일 행렬 A와 b가 x의 함수가 아닌 특정한 숫자들로 구성되어 있다면 x는 A의 역행렬(inverse matrix)을 계산하여 쉽게 계산할 수 있다. 하지만 A나 b가 구하고자 하는 x에 무관하지 않고 x에 따라 변하는 값을 가진다면 이야기는 달라진다. 다시 말해 x를 알아야 A나 b를 결정할 수 있기 때문에 계산이 단순하지 않다. 이러한 경우가 바로 비선형(nonlinear) 문제에 해당된다.
이러한 비선형 방정식은 한번의 계산으로 해답을 구할 수 없기 때문에 반복계산(iterative calculation)을 하여야 한다. 즉, 구하고자 하는 x값을 미리 추정하고 이 추정 값을 가지고 A와 b을 결정한 다음 x값을 계산한다. 그리고 계산된 x값으로 다시 A와 b를 결정한 다음 다시 x값을 계산하는 일련의 반복과정을 거치게 된다. 이렇게 반복적으로 계산을 하면 대부분의 경우 x는 정답에 가깝게 된다. 이러한 반복계산에 있어 가장 큰 관심사는 원하는 정확도를 가지는 해답 x를 얼마나 적은 반복계산으로 구할 수 있느냐이다. 이를 위한 많은 반복계산 기법들이 연구자들에 의해 제안되었으며, 그 중에서 가장 효과적인 방법이 바로 뉴튼-랩슨 반복계산 기법이다.
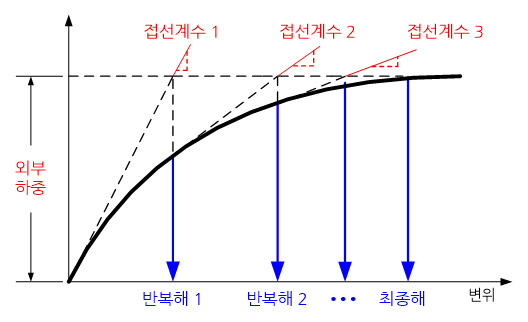
이 기법은 반복계산 횟수를 최소화 시키기 위해 매 반복계산 시 정답에 도달하는 가장 빠른 방향으로 A와 b를 결정한다. 하지만 행렬방정식의 크기가 큰 경우에는 반복과정 시 매번 A나 b를 계산하는데 걸리는 시간이 증가하기 때문에 단순히 최초 계산에서 결정한 A나 b를 사용하기도 한다. 이렇게 단순화 된 반복계산 기법을 수정된 뉴튼-랩슨 기법(modified Newton-Raphson method)이라고 부른다.
.