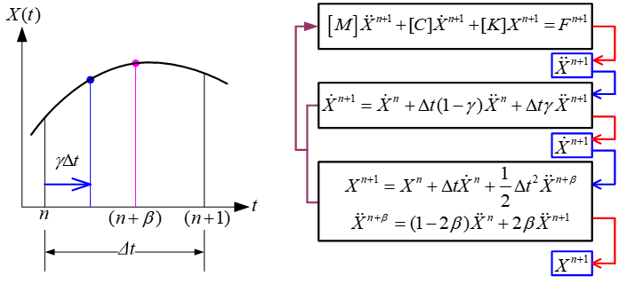점성(viscosity)을 포함한 일반화된 뉴튼의 제2법칙은 물체의 가속도, 속도 및 동적 변위를 수학적으로 표현한 미분방정식이다. 이러한 운동방정식을 수치해석(numerical analysis)적으로 푼다는 것은 각 시점에서 물체의 가속도, 속도 및 동적 변위를 구하는 것이다. 관심의 대상이 되는 시간 구간 동안, 이들을 구하기 위해서는 이들에 대한 초기 시점에서의 값, 즉 초기조건(initial condition)으로부터 시작하여 세분화된 각 시점에서의 값들을 순차적으로 계산하여야 한다.
수학적인 관점에서 본다면 미분방정식을 시간에 대해 적분하는 것이기 때문에, 각 시점에서 이들의 값을 순차적으로 계산하는 과정을 시간적분(time integration)이라고 부른다. 시간적분에는 크게 명시적 기법(explicit method)과 암시적 기법(implicit method)이 있는데, 뉴마크기법은 대표적인 암시적 시간적분 기법이다. 이 기법은 미국 일리노이 대학의 나단 뉴마크(Nathan Newmark, 1910~1981) 교수에 의해 소개되었으며, 일반적으로 뉴마크 베타 기법(Newmark beta method) 혹은 일정 평균가속도 기법(constant averaged acceleration method)이라고 불린다.
이 기법은 중앙차분법(central difference method)과 같은 명시적 시간적분법과는 달리 시간간격(time step)과 요소크기(element size)에 무관하게 항상 해의 수렴성(convergence)과 해의 안정성(stability)이 보장된다. 하지만 질량행렬(mass matrix)을 대각화 하지 않고 전체 행렬을 그대로 유지한 채 행렬계산을 수행하기 때문에 해석시간이 길어지는 단점을 지니고 있다. 이러한 이유로 지금과 같이 대형 동해석 문제를 주로 다루는 상황에서는 그 사용빈도가 줄어들고 있다. 참고로 뉴마크기법에서는 베타(beta) 그리고 감마(gamma)라고 하는 두 개의 변수를 포함하고 있는데, 일반적으로 베타는 1/4 그리고 감마는 1/2을 취한다.
.