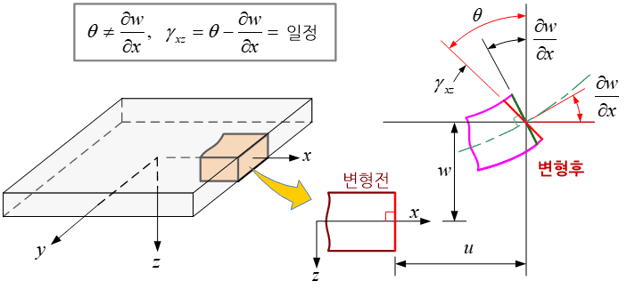
박판 구조물(thin-walled structure)의 유한요소 해석에 주로 사용되는 평판 요소(plate element)나 쉘 요소(shell element)는 민들린-라이즈너 이론에 기초하고 있다. 이 이론은 두께가 충분히 작다고 가정한 박판 구조물에 대한 가장 오래 된 이론인 킥컵-러브 가설(Kirchhoff-Love postulates)을 미국의 공학자 민들린(Raymod Mindlin, 1906-1987)과 독일의 라이즈너(Hans Reissner, 1874-1967)가 보완한 것이다.
킥컵-러브 이론은 두께가 무한히 작지 않은 경우에는 두께 방향으로 전단 변형률(shear strain)과 전단 응력(shear stress)을 무시할 수 없기 때문에 그 정확성이 현저히 저하된다. 하지만, 민들린-라이즈너 이론에서는 구조물의 두께 방향으로 일정한 크기의 전단 변형률과 전단 응력을 허용하고 있다. 따라서, 두께가 작지 않은 구조물 해석에 적용이 가능하다. 하지만 이 이론도 구조물 두께방향으로의 전단 변형률과 전단 응력을 일정한 크기로 가정하였기 때문에 정확한 분포와는 어느 정도 거리가 있다.
구조물의 두께 방향으로의 전단 변형률과 전단 응력의 정확한 분포는 중립축(neutral axis)에서 최대가 되고 아래 윗 면에서는 0의 값을 갖는 타원 형태이다. 민들린-라이즈너 이론의 이러한 모순을 보완하기 위하여 전단 변형률로부터 전단 응력을 계산하는 과정에 전단 보정계수(shear correction factor)를 도입하고 있다. 평판 요소나 쉘 요소에서 이 보정계수를 필요로 하는 이유가 바로 이 때문이며 일반적으로 5/6의 값을 채택하고 있지만, 정확히는 부재의 단면적과 두께의 함수로 표현된다.
.