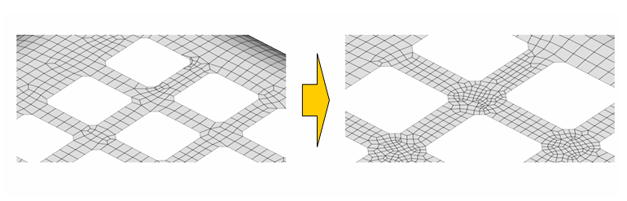
임의 자연현상을 유한요소해석(finite element analysis)과 같은 시뮬레이션을 통하여 해답을 구하게 되면 이 해답은 정담이 아니라 근사해(approximate solution)이다. 따라서 반드시 정답과의 차이, 즉 오차(error)가 발생하게 된다.
이 오차를 줄이기 위해서는 문제 영역을 세분화 시킨 유한요소(finite element)의 개수를 증가시키거나 보간함수(interpolation function)의 차수를 증가시켜야 한다. 해가 특이성(singularity)을 나타내는 영역에는 전자가 효과적이며, 그렇지 않고 해가 완만한 변화를 보이는 영역에는 후자자 효과적인 것으로 알려져 있다.
대부분의 경우, 목표로 하는 정확도를 가지는 근사해를 구하기 위해 필요한 요소의 개수나 기저함수(basis function)의 차수는 해석결과를 구하기 전에는 알 수 없다. 따라서 해석을 수행하기 전에 문제영역 전체를 동일한 보간함수 차수를 가진 유한요소들로 균일하게 세분화 한다. 그런 다음 필요에 따라 오차평가(error estimate)를 수행하고 이 오차정보에 따라 필요한 영역에 유한요소 개수를 증가시키거나 기저함수의 차수를 높이게 된다.
이렇게 근사해의 정확도를 향상시키기 위하여 유한요소의 개수를 증가시키는 것을 요소망 세밀화라고 부른다. 참고로 일정한 크기의 문제 영역 내에 유한요소의 개수를 증가시킨다는 것은 결국 유한요소의 크기를 줄이는 것이다. 요소망 세밀화는 문제 영역 전체에 걸쳐 수행할 수도 있고, 오차가 높은 국부 영역에만 한정하여 수행할 수도 있다. 하지만 효율성 측면에서 후자의 방식이 일반적으로 사용되고 있다.
다른 한편, 초기 적용한 요소망이 너무 조밀하여 유한요소의 개수를 감소시키는 경우도 있는데, 이러한 경우를 요소망 비세밀화(mesh unrefinement)라고 부른다.
.