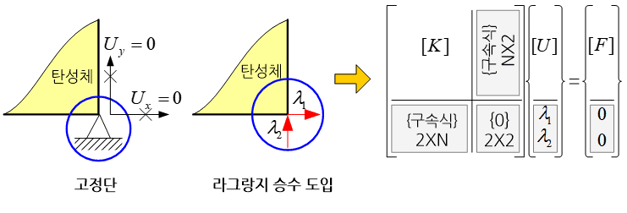
자연계에서 발생하는 물리적 현상들 중에는 물체의 기하학적 형상, 거동 혹은 재질 등이 반드시 만족해야 하는 구속조건(constraint)을 가지는 경우가 있다. 이러한 문제를 이론적으로 푸는 경우에는 이 구속조건을 정확히 반영할 수 있지만, 유한요소 해석(finite element analysis)과 같은 수치해석(numerical analysis)에서는 정확하게 만족시키기 어렵기 때문에 근사적으로 만족시키는 벌칙기법(penalty method)이 보편적으로 사용되고 있다.
하지만 구속조건을 정확하게 만족시켜야 하는 문제에 대해서는 라그랑지 승수법을 적용하면 가능하다. 이 기법은 라그랑지 승수(Lagrange multiplier)를 구속조건에 대한 미지수로 추가하여 물리적 현상을 수치해석적으로 풀게 된다. 그 결과 행렬방정식의 크기가 증가할뿐더러 해석에 걸리는 시간도 증가하는 단점을 안고 있다. 이 기법의 물리적 의미는 라그랑지 승수라는 가상의 힘을 구속조건이라는 물리량에 가하여 이들의 곱을 물체의 내부 에너지에 더하는 것이다. 구속조건을 근사적으로 만족시키는 벌칙기법과는 서로 상반되는 장단점을 지니고 있다. 참고로 구속조건의 개수만큼 미지수의 개수도 증가한다.
예를 들어 해석 대상의 물체가 비압축성(incompressibility) 재질이라면 이 조건을 만족시키기 위해서는 각 유한요소(finite element), 유한요소 내 각 절점(node) 혹은 각 수치 적분점(integration point) 마다 구속조건을 적용해야 하기 때문에 미지수의 크기는 엄청나게 증가하게 된다. 하지만 벌칙기법에서는 구속조건의 개수와 무관하게 미지수가 증가하지 않기 때문에 구속조건에 따른 미지수 증가가 문제시 되는 경우에 매우 효과적이다.
.