강재와 같이 결정체로 이루어진 금속이 외부로부터 하중을 받아 영구적인 변형, 즉 소성변형(plastic deformation)을 일으키는 응력(stress)의 크기를 항복응력(yield stress)이라고 한다. 그리고 소성변형에 따라 금속 내부 결정체의 미끄러짐 혹은 전이(dislocation)에 의해 항복응력이 증가하는 현상을 재료의 경화(hardening)라고 부른다.
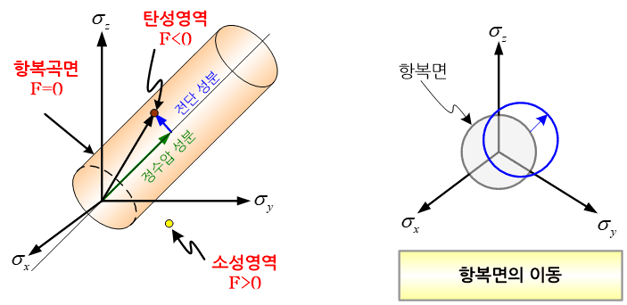
임의 물체의 항복은 한 방향으로의 응력 성분만의 크기로 결정되는 것이 아니라, 직교하는 3축 방향으로의 응력성분들의 조합에 의해 결정된다. 3차원 공간 상에서 X, Y 그리고 Z축을 설정하고 항복이 시작되는 응력의 상태를 나타내면 구(sphere) 혹은 다각형(polygon) 형상의 곡면이 된다. 그리고 이 곡면을 특별히 항복곡면(yielding surface)이라고 부른다.
물체 내 임의 지점에서의 응력상태가 이 구 혹은 다각형 내부에 속한다면 그 지점은 아직 항복이 발생하지 않은 탄성영역 내에 있다. 하지만 물체 내 어떤 지점에서의 응력상태가 이 항복곡면 외부에 속한다면 이 지점에서는 이미 항복이 시작되었다. 그런데 앞서 언급한 재료의 경화가 발생하면 이 항복곡면은 팽창하게 되에 항복응력이 증가하게 된다.
항복곡면이 팽창하는 형태는 모든 방향으로 같은 크기로 팽창하는 경우, 각 방향으로 각기 다른 크기로 팽창하는 경우, 그리고 곡면의 크기는 일정한 채 그 중심이 이동하는 경우로 구분할 수 있다. 첫 번째 경우를 등방성 경화(isotropic hardening), 두 번째 경우를 이방성 경화(anisotropic hardening), 그리고 마지막 경우를 이동성 경화라고 부른다. 그리고 이러한 경화 거동을 수학적으로 표현한 모델을 경화법칙(hardening rule)이라고 부르며, 이동 경화를 수학적으로 표현한 수식을 이동 경화법칙이라고 한다.
.