우리 주위에서 흔히 볼 수 있는 여러 가지 현상들은 각기 그 거동을 지배하는 인자들이 존재한다. 그리고 그 현상과 인자들과의 관계를 수학적으로도 표현할 수 있다. 그리고 거동에 영향을 미치는 인자들 사이에도 서로 상관관계가 존재하는 경우가 종종 있다. 그런데 상관관계를 가지는 인자들 사이의 관계 역시 수학적인 표현이 가능하기 때문에, 위에서 말한 거동은 어떠한 인자들로 표현하느냐에 따라 수학적 표현이 달라질 수 있다.
하지만, 서로 다른 수학적 표현일지라도 그 표현에 포함되어 있는 인자들 사이의 관계를 통하여 서로 변환(transform)이 가능하다. 이렇게 상관관계를 가지는 인자들로 표현되는 서로 다른 수학적 표현들 사이의 변환은 19세기 독일의 위대한 수학자 칼 구스타프 자코비(Jacobi, 1804-1851)에 의하여 최초로 연구되었다.
위에서 말한 현상은 특정한 학문분야에 한정되지 않고 모든 문제에 대해서도 동일하게 적용된다. 만일 그 거동이 물체의 공간상의 좌표일 경우에는 이 변환을 좌표변환(geometry transformation)이라고 부르고, 만일 수학적인 함수일 경우에는 함수변환(function transformation)으로 불린다. 이러한 거동을 상관관계를 가지고 있는 서로 다른 인자들에 의한 함수들로 표현하였을 경우, 이 함수들 사이의 변환은 자코비 행렬(Jacobi matrix)를 통해서 가능하다.
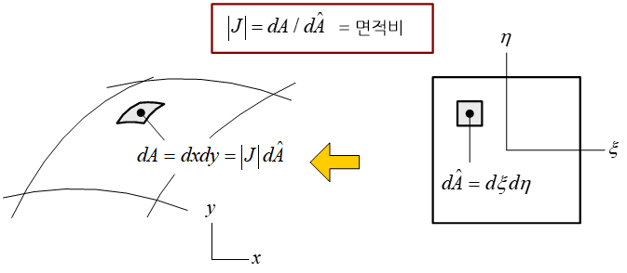
자코비 행렬과 자코비언이란 용어는 수학자 자코비의 이름을 따서 명명하게 되었다. 물체의 기하학적 형상에 대한 좌표변환에 있어 자코비언의 물리적 의미는 다음과 같다. 1차원 형상의 경우에는 변환 관계에 있는 두 직선의 길이 비를, 2차원의 경우에는 변환 관계에 있는 두 평면의 면적 비, 그리고 3차원의 경우에는 부피 비를 의미한다. 따라서 이러한 물리적 특성에 따라 좌표변환에 있어 자코비언은 0이나 음(-)의 값을 가질 수 없다.
.