시간에 따라 변하는 물체의 거동을 풀기 위해서는 물체의 거동을 지배하는 수학적 표현, 즉 미분 방정식을 시간에 대해 적분해야 한다. 하지만 이러한 시간 적분은 수학의 적분공식을 이용한 이론적 방법에서는 가능하지만 수치해석(numerical analysis)에서는 불가능하다. 왜냐하면, 수치해석은 물체의 거동을 보간함수(interpolation function)를 이용하여 근사하고, 이 근사식을 수학적 표현식에 대입하여 행렬방정식으로 전환시켜 근사해(approximate solution)를 구하기 때문이다.
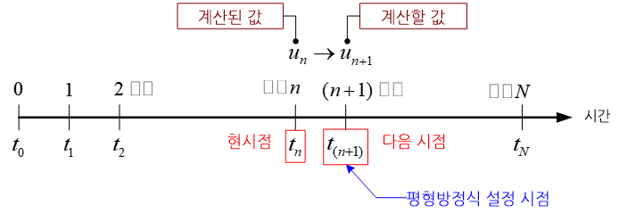
시간에 따라 변하는 물체의 거동을 수치해석을 통하여 구하기 위해서는 전체 시간 구간을 유한 개의 시점으로 나눈 다음, 초기값을 이용하여 각 시점에서의 물체의 거동을 순차적으로 계산해 나가야 한다. 다시 말해, n번째 시점에서의 거동값을 계산하여 알고 있다면, 이 값을 행렬 방정식에 대입하여 (n+1)번째 시점에서의 거동값을 계산한다.
이렇게 순차적으로 각 시점에서의 거동값을 계산해 나가는 수치기법을 시간적분(time integration)이라고 부르고, 수학적 표현식을 어떤 시점에 두고 계산하느냐에 따라 크게 두 가지 적분 방식, 즉 암시적 시간적분과 명시적 시간적분(explicit time integration)으로 구분된다. 암시적 시간적분은 거동의 수학적 표현식을 (n+1)번째 시점에 놓고 푼다. 그런데 (n+1) 시점에서의 값들은 미지수이기 때문에 복잡한 계산 방법을 거치고 되고, 그 결과 시간적분을 위해 소모되는 시간이 명시적 시간적분보다 길다는 단점이 있다.
하지만, 시간에 따른 물체 거동의 안정적인 응답을 구할 수 있어 해석결과의 정확도가 상대적으로 높고, 요소 크기(element size)나 시간 간격(time step)에 대한 제약조건이 없다는 장점을 지니고 있다. 따라서, 풀고자 하는 해석 문제의 크기가 그다지 크지 않은 경우라면, 암시적 시간적분을 사용하는 것이 유리하다.
.