수학적 측면에서 조화함수는 2번까지 미분이 가능한 함수들을 지칭한다. 잘 아는 바와 같이 미분이 가능하기 위해서 함수는 연속적이어야 하고, 우리가 잘 알고 있는 사인(sine) 및 코사인(cosine) 함수는 끝없이 미분이 가능한 함수들이다. 이처럼 몇 번까지 미분이 가능하냐는 그 함수의 매끈함(smoothness)을 나타내는 척도로 사용된다.
한편, 매끈한 함수는 수학, 자연과학 및 공학분야에 있어 매우 유용하게 사용되고 있다. 왜냐하면 테일러 급수전개(Taylor series expansion)와 같은 주요한 수학적 도구들은 무한 차수까지 미분이 가능한 함수들을 사용하고 있기 때문이다. 사인 및 코사인 함수가 퓨리에 급수전개(Fourier series expansion)에 사용되는 이유가 바로 여기에 있다.
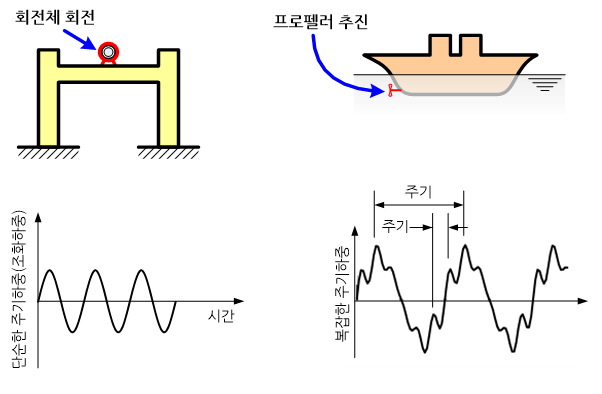
한편, 모든 자연현상이나 물체의 거동은 테일러나 퓨리에 급수로 표현이 가능하다. 예를 들어 물체에 가해지는 임의 동적하중(dynamic load)은 무한개의 주기가 서로 다른 사인과 코사인 파의 조합으로 표현이 가능하고, 이러한 외란을 받는 물체의 동적 거동 역시 주기가 서로 다른 무한개의 사인과 코사인 함수들의 조합으로 표현이 가능하다. 동적 시스템의 고유한 진동특성을 나타내는 고유진동수(natural frequency) 및 고유모드(natural mode)를 구하기 위해 물체의 동적 거동을 이들 함수로 가정하는 이유도 이러한 수학적 원리에 기초한다.
하나의 주기를 가진 순수한 조화가진은 거의 찾아보기가 힘들며, 거의 대부분 매우 복잡한 형태를 지닌 임의 가진(random excitation) 혹은 순간적으로 가해지는 극단적인 임펄스(impulse) 등이다. 하지만 이러한 가진들도 위에서 언급한 함수들의 조합으로 표현이 가능하다.
.